Физико-математические науки
Lyahov V.V.
PhD, leading research scientist, Institute of Ionosphere
National Center of Space Research and Technology, Almaty
Neshchadim V.M.
PhD, leading research scientist, Institute of Ionosphere
National Center of Space Research and Technology, Almaty
ON COMPLEXIFICATION OF PHYSICS. COMPLEX NUMBERS AS OBJECT OF PHYSICAL REALITY
Abstract: Now in physics, the paradigm dominates: real numbers correspond to physical quantities. However, modern physics has accumulated many examples of the opposite kind when complex numbers are used as objects of physical reality. In this paper, we have attempted complexification of physics. An extension of the Archimedean ordered field of real numbers to a non-Archimedean ordered field of complex numbers is carried out. It is possible that the imaginary part, being unobservable, at the same time must be inherent in a physical quantity, being something of a hidden parameter, and is manifested only indirectly, forcing the system to move along one or another path.
Keywords: complexification of physics, physical reality, complex numbers, non-Archimedean complex numerical axis, nonstandard analysis, mechanical oscillator.
1. At the stage of semi-recognition of complex numbers
1.1. Introduction to the problem.
Since its inception, complex numbers have fully become part of mathematics whereas physics is now in the stage of semi-recognition of complex numbers. On the one hand, physics, using the mathematical apparatus, manipulates complex numbers. On the other hand, common sense recommends that all observed quantities are associated exclusively with real numbers. It is assumed that the complex calculus has only an auxiliary, formal-mathematical character. The course of reasoning of the modern physicist is this: «We live in the real world. Therefore all quantities should be described by real numbers.» It seems that this statement is completely natural and does not require any additional justification. This provision is an example of a paradigm and natural scientists, in fact, take it on faith. They say that the whole development of science confirms this thesis.
However, one can give the opposite examples.
The relativity theory introduces imaginary time . Moreover, only in this form, together with three spatial coordinates, it forms a four-dimensional space-time. The fourth axis of space-time is an imaginary quantity. On the one hand, in the theory of relativity, it is always emphasized the conditional character of imaginary time. However, on the other hand, it is also always noted that for the first time a deeply essential connection of space and time was discovered.
It is said that the main object of quantum mechanics, i.e., complex-valued wave function, does not have a physical meaning, but its square has it. Already this conclusion disturbs us. Moreover, it turns out that the quantum-mechanical principle of superposition should use namely a wave function that does not have a physical sense, and not its square, which has this sense.
In relativistic quantum mechanics, mathematical considerations of the necessity of completeness of the system of wave functions forced us to introduce a concept of the levels of negative energy. However, the energy of a resting particle can be negative only if either a negative value is assigned to mass or an imaginary value is assigned to light speed. Dirac gives the physical interpretation of this result of the formal mathematical apparatus. He postulated the principle nonobservability of states with negative energy because particles occupy all levels with negative energy, and therefore no transitions between any two levels that could be observed are possible (vacuum state). However, postulating first the principle nonobservability of such states, physicists then talk about the interaction of a hydrogen atom with a vacuum (Lamb shift). Does this mean that the background of filled states with negative energy – vacuum – nevertheless manifests itself in reality?
When solving a differential equation, we first have to solve the so-called characteristic equation. This equation is algebraic, and its solution is sought on the field of complex numbers. In the theory of oscillations, for example, such quantities as the frequency and the wave vector, and therefore their reciprocals — the period of oscillations and the wavelength, become complex-valued.
1.2. Statement of the problem
In the light of the preceding, it would be logically correct to take the next step. Supposing that the physical quantities correspond, “in the main,” to the real axis, at the same time, consider the complex neighborhood of the real axis and to investigate in this neighborhood the questions of the limiting transition. We have to allow an initial possibility of the existence of complex physical quantities. This assumption saved us from the need to interpret the suddenly emerging imaginary somehow and had happened more than once when the reality of physical quantities was postulated. The proposed program must be fulfilled if we want that the basic operations on quantities do not lead them out of their field in all domains of application of mathematics.
In our opinion, all of the above requires the complexation of physics, and further theoretical consideration will show what it will lead to. In fact, the complexification is reduced to the assumption of the complexity of all quantities in all physical laws. The real parts of the quantities are assumed to be measurable. Let us try to find out theoretically whether a situation is possible when the solution for the real part of the introduced complex quantities differs significantly from the usual real solution determined by the equations of some physical law.
The subject of our research will be differential equations — the basis for modeling physical processes. In practice, no value can be accurately measured or specified, all quantities fluctuate. In the region of real numbers, to date, a stability theory has been developed based on the Lyapunov approach [1] that allows us to investigate the dependence of the solution of the problem on the fluctuations of the additional conditions.
It is proposed to extend the Lyapunov stability method to the complex plane in order to study the dependence of the solution on the fluctuations of the imaginary parts of the additional conditions in a neighborhood of zero. Will it be preserved in this case the continuity of the solution to the change on the initial conditions? It is natural to begin research with the simplest objects and laws of physics, solving particular problems.
1.3. Research of the equations of classical physics
Any equation contains three kinds of elements: functions, arguments, and coefficients. The statement of the problem requires, in general, to consider all elements as complex-valued.
The linear equation of the first order with constant coefficients.
Equation
![]() (1)
(1)
describes the phenomena of radioactivity, light absorption, absorption of -rays, phase equilibrium (the Clapeyron-Clausius equation). That is an autonomous equation, where the function N, the argument t, and the parameter are complex-valued. We consider the Cauchy problem
![]() (2)
(2)
with the aim of investigating the effect of small imaginary parts of the initial conditions and parameters on the real part of the solution.
The solution of problem (1), (2)
![]() (3)
(3)
is investigated numerically in the complex domain. The results of the solution are shown in Fig. 1 5. Calculations are carried out for the half-life of T1/2 = 10 days (![]() = ln2/T1/2). The relations of imaginary parts to real parts for all quantities were taken to be the same:
= ln2/T1/2). The relations of imaginary parts to real parts for all quantities were taken to be the same:
 (4)
(4)
Fig. 1a (J/R= 0) demonstrates the usual law of radioactive decay. The phase portrait in the coordinates {N, dN/dt }, shown in Fig. 1b is a stable node.

Fig. 1a. The law of radioactive decay(J/R= 0)
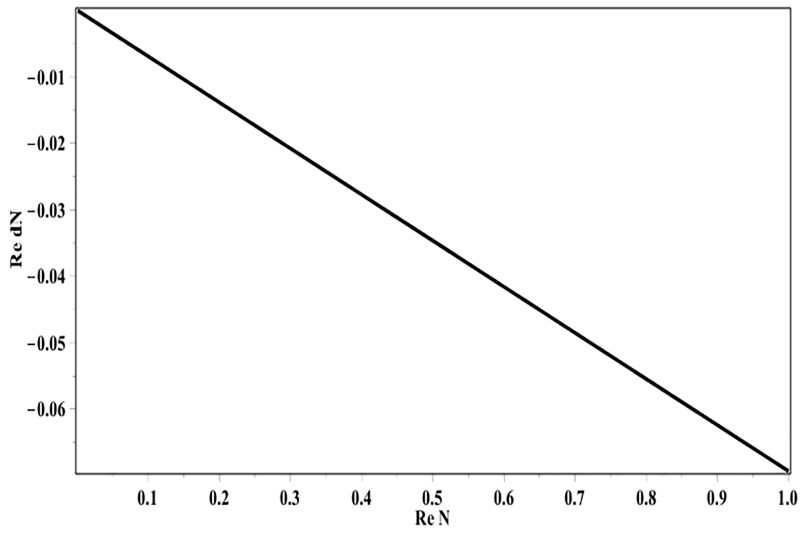
Fig. 1b. Phase portrait, radioactive decay (J/R= 0)
In Fig. 2. (J/R= 0,3) — deviation from the known law of radioactive decay is already clearly visible. When the parameter J/R passes through zero, the first bifurcation occurs: the stable node turns into a stable focus.
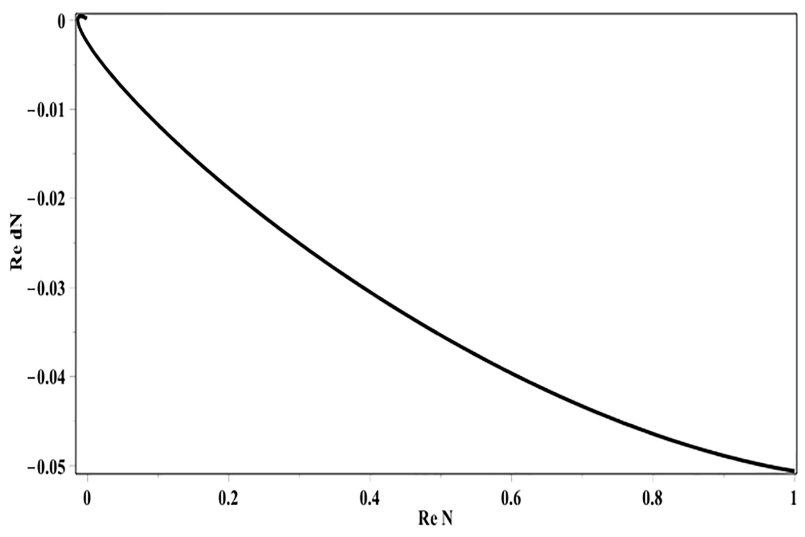
Fig. 2. Phase portrait, radioactive decay (J/R= 0,3)
Fig. 3 (J / R = 0.9) shows a well-defined stable focus.
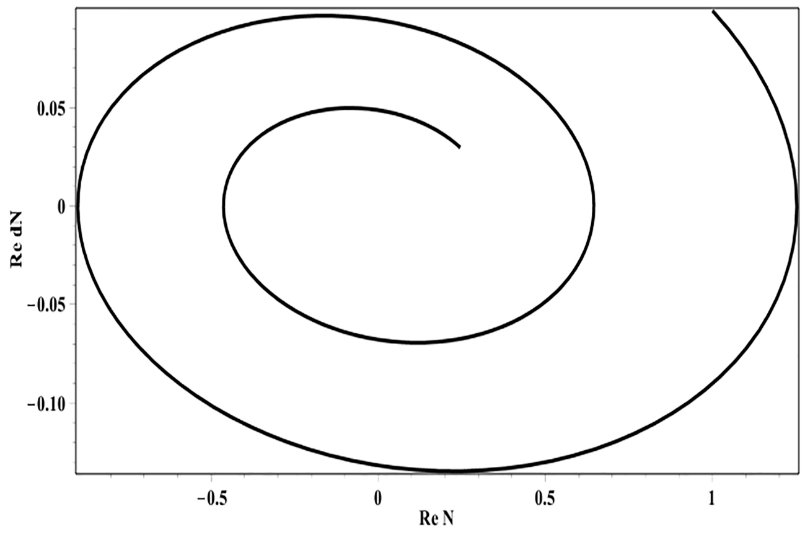
Fig. 3. Phase portrait, radioactive decay (J/R= 0,9)
For J / R = 1 (see Fig. 4), a second bifurcation — the Hopf bifurcation — occurs: a stable focus turns into a limit cycle.
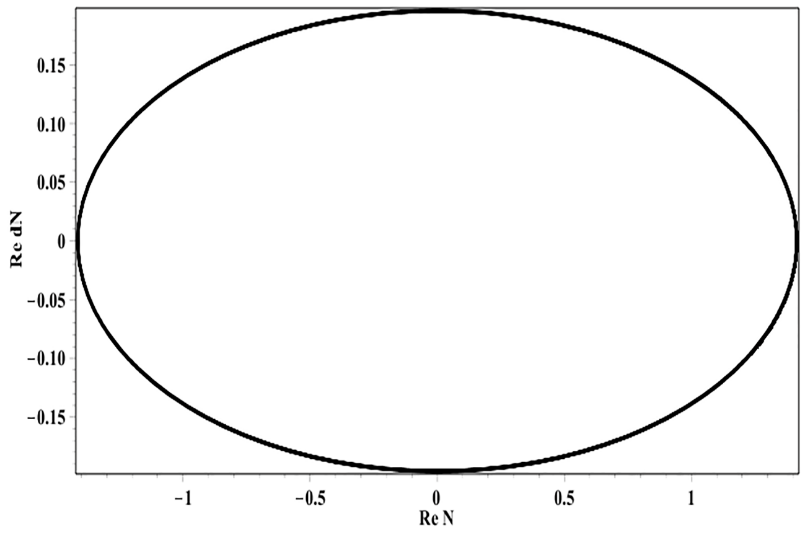
Fig. 4. Phase portrait, radioactive decay (J/R= 1)
At the J/R= 1,01 value (see Fig. 5), the third bifurcation takes place: the limit cycle becomes an unstable focus.
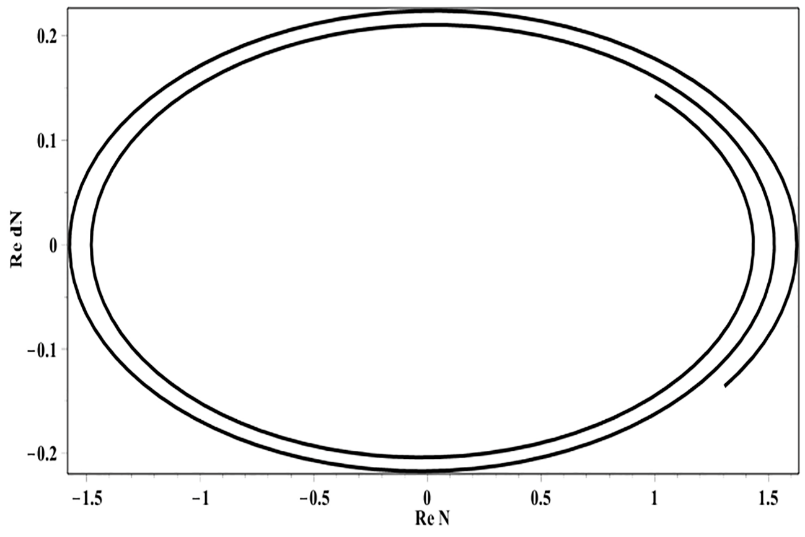
Fig.5. Phase portrait, radioactive decay (J/R= 1,01)
As far as we know, the phenomenon of bifurcation of solutions has always been associated with the nonlinearity of the equations, but the simplest possible linear equation (1) in the complex plane also shows the bifurcation property.
The second and third bifurcations considered above occur at large J/R values and are interesting, therefore, only from a mathematical point of view. However, the first bifurcation, which takes place in a neighborhood of J/R=0, can have physical content. Even small imaginary parts of the coefficients and initial conditions (J/R≈0) lead to a qualitative rearrangement of the real part of the solution, transforming the stable node into a stable focus.
1.4. Conclusions
Other equations of classical physics are considered in papers [2, 3, 4]. The basic and most definite laws of classical physics, defined in the sense that the quantities are appearing in them, are determined strictly, with a minimal degree of subjectivity, are investigated, and these quantities can be measured with a high degree of accuracy.
Simple objects, such as a rotator, Newton’s equation with the constant force, are stable concerning complex-valued perturbations in a neighborhood of zero. With a loss of simplicity of the objects, stability is lost.
In linear equations, fluctuations of the imaginary part of the coefficients in a neighborhood of zero lead to bifurcations of the real part of the solution. It was found that a small imaginary part can direct a solution to the real axis. This fact is interesting from a formal mathematical point of view, even more, actual is its interpretation in the physical and philosophical aspects. It is possible that the small imaginary part, being unobservable, is at the same time necessary for physical quantity, being something of a hidden parameter, and manifests itself only indirectly, forcing the system to move along one or another path.
Similar ideas about the relationship between complex quantities and physical reality are developed in the paper [5].
2. On complexification of physics.
2.1. Introduction
So, the number. “Without having overcome their difficulties with irrational and negative numbers, the Europeans added to their burdens by blundering into what we now call complex numbers.” [6]. Using an imaginary unit ![]() , a mathematician or physicist does not perceive this object; it is impossible to perceive or understand it, to imagine it as clearly as, say, a natural number. Moreover, yet, starting from the language background: “imaginary” means “non-existent.”. How so: there is a non-existent number?
, a mathematician or physicist does not perceive this object; it is impossible to perceive or understand it, to imagine it as clearly as, say, a natural number. Moreover, yet, starting from the language background: “imaginary” means “non-existent.”. How so: there is a non-existent number?
Now it is believed that real numbers correspond to physically measurable quantities, only the formal mathematical and auxiliary character is assigned to the complex calculus in physics. The development of natural science indicates that objects that existed previously only as mathematical, «ideal» concepts were filled with time with real content and accepted into the family of physical objects. Examples are negative and irrational numbers. Now it is possible to describe physical quantities with negative and irrational numbers.
Historically, there has been a gradual expansion of number fields. The field of natural numbers was extended to the field of integers, then to the field of rational numbers, then to the field of real numbers and, finally, to the field of complex numbers. In this case, the complex field has a fundamental feature that distinguishes it: it is algebraically closed. The restriction of physical quantities only to the field of real numbers seems logically unsatisfactory since often mathematical operations derive them from the field of the original definition.
By complexing physics and trying to find the possibility of experimental verification of the complexness of physical quantities, we must not forget that two complex quantities in physics have already been introduced. Introduced ![]() — complex frequency and mass
— complex frequency and mass ![]() . The frequency is introduced in classical physics, more precisely in plasma physics and is associated with the so-called collisionless Landau damping, the mass is introduced in quantum electrodynamics, in perturbation theory.
. The frequency is introduced in classical physics, more precisely in plasma physics and is associated with the so-called collisionless Landau damping, the mass is introduced in quantum electrodynamics, in perturbation theory.
Here arises a cardinal question about the relationship between the concepts of magnitude and number. It seems natural to adopt the following definition, which was expressed, for example, by A.N. Kolmogorov [7]: the number is the ratio of two quantities. With this definition, the very fact of the existence of complex numbers immediately leads to the conclusion about the existence of complex quantities. However, the main property of the quantities is to be more or less, that is, to be ordered. Consequently, complex physical quantities, as well as their corresponding complex numbers, must be ordered structures.
2.2. The ordering of the field of complex physical quantities
Taking into account the above, we order the field of complex numbers. From Zermelo’s theorem, it follows that any set can be even completely ordered, and the number of ways of ordering is infinite. We order the set of complex numbers in the following way, hoping that this corresponds, to some extent, to the objectively existing ordering of complex physical quantities.
We assume (see Fig. 6) that for z’ = x’ + iy’ and z» = x»+ iy»
 (5)
(5)
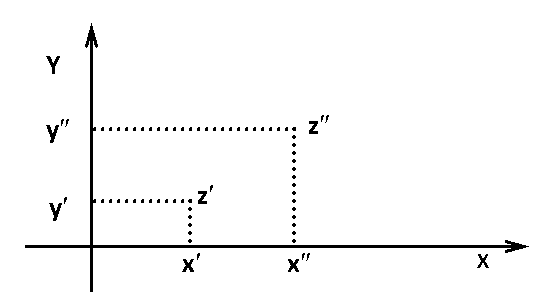
Fig.6. Complex plane
If we denote by the ordinal type of the set of all real numbers, then the set of complex numbers is ordered by type 2 (lexicographically).
The above method of ordering the set of complex numbers is well known, and here this formalism is put by the definition of complex physical quantities. If we arrange all points of the set of complex numbers of the order type 2, on the line (plane design on the line), then we get a complex non-Archimedean number line because it contains uncountable many non-overlapping segments, namely, the power of this set of segments is the power of the continuum. The set of points of any vertical line in Fig. 6 can be mapped onto the complex axis in the form of a segment of arbitrary length; for this, we choose some segment as such.
2.3. Non-Archimedean complex numerical axes
In ordinary analysis and geometry, only archimedean right lines are considered, that is, those that contain non-overlapping segments only in a countable number. All points of ordinary archimedean right lines are valid.
The desire to follow the logic of determining the concept of a number as a ratio of two quantities and the ordering of the set of complex numbers leads to the fact that each physical quantity is located on the corresponding non-Archimedean complex numeric axis (see Fig. 7).
The interval β is a region of complex numbers of the form -x ±iy; the interval is the domain of complex numbers of the form x iy; the segment α0 is the region of imaginary numbers, the points of this segment are connected one-to-one with the points of the imaginary axis![]() Every real number x of a non-Archimedean complex numeric axis is surrounded by a field of complex points of the form ±iy +x of the corresponding segment α .
Every real number x of a non-Archimedean complex numeric axis is surrounded by a field of complex points of the form ±iy +x of the corresponding segment α .
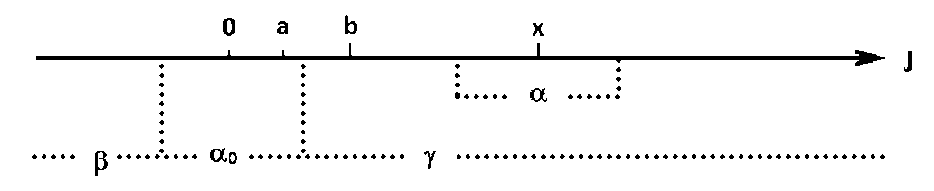
Fig. 7. Non-Archimedean complex number axis
Of all the existing physical quantities, three have a special value –time, space and mass. In mechanics, at least, all other quantities can be expressed regarding these three basic quantities. As follows from the above analysis, each of the three quantities is located on the corresponding non-Archimedean complex numerical axis. That leads to a violation of the law of conservation of energy in our usual world of real numbers.
The last conclusion can be illustrated by an example of the simplest mechanical system — the ideal classical oscillator
![]()
All values here are complex. The conserved quantity is the complex energy — the first integral of this equation:
 (6)
(6)
Using the explicit complex form of the quantities from (6) we obtain:
 (7)
(7)
From the complex relation (7) it follows that the equalities must be satisfied separately:
![]() (8)
(8)
So only in the case of small imaginary parts ![]() , expression (8) coincides with our usual relation:
, expression (8) coincides with our usual relation:
 (9)
(9)
In the world of complex quantities, energy is also a complex quantity that retains its value. The energy composed on real quantities, as can be seen from expression (7), is not conserved for non-zero imaginary values and tends to a constant, only for ![]() .
.
One can try to explore the foundations of the geometry and physics of the new reality that arose when non-Archimedean complex numeric axes were introduced. First of all, note that the ordering of the elements of this new reality (5) coincides with the usual ordering of the elements on the real numerical axis for y’ = y»=0. Veronese and Gilbert created non-Archimedean geometries. In non-Archimedean geometry, one can not characterize the ratio of two segments using ordinary numbers. Hilbert [8] developed the geometric calculus of segments, without any relying on the concept of a number, and constructed a geometry, eliminating the axiom of continuity, which is in close connection with the Archimedes’s axiom. Moreover, Veronese came out to generalize the Dedekind definition of continuity [9].
The Archimedes’s axiom on a non-Archimedean complex numeric axis is not satisfied, that is, one can not find such a large natural number N, that Na> b if a <b (see Fig. 7). Therefore, the set of points of a segment α of a non-Archimedean complex axis J can be likened to a set of actual infinitesimal numbers of non-standard analysis. The real points of this axis play the role of standard numbers of non-standard analysis. The segment α , being a non-standard neighborhood of the standard number, has the meaning of a monad of non-standard analysis. The difference of the complex non-Archimedean axis introduced by us from the usually considered hyperгеal axis consists in the fact that in this case, the monad consists of imaginary numbers. If the actual existing infinite small number of the monad of the nonstandard analysis is denoted as ε , then in the proposed complex nonstandard analysis this number will have the form iε, where i— is the imaginary unit.
We adopt the following definition. The element iε of an ordered field is infinitesimal if the following condition is satisfied:
![]() and further. (10)
and further. (10)
The number iε can be multiplied by itself and by any real number. The set of numbers thus obtained is algebraically closed. Moreover, if we want to preserve all the properties of complex numbers, then it must be assumed that on the non-Archimedean complex numeric axis, even powers of this number![]() , where k = 1, 2, 3, … translate it from the status of the actual small to the status of the standard (real) number. It is this situation can lead to absolutely unusual results if to describe the real-life world by the offered mathematical model of a complex non-Archimedean axis. A non-Archimedean complex numerical axis, by analogy with a hyperreal one, is called hypercomplex. A non-Archimedean complex numeric axis can be considered as an accomplished example of an ideal mathematical object — the field of hypercomplex numbers.
, where k = 1, 2, 3, … translate it from the status of the actual small to the status of the standard (real) number. It is this situation can lead to absolutely unusual results if to describe the real-life world by the offered mathematical model of a complex non-Archimedean axis. A non-Archimedean complex numerical axis, by analogy with a hyperreal one, is called hypercomplex. A non-Archimedean complex numeric axis can be considered as an accomplished example of an ideal mathematical object — the field of hypercomplex numbers.
2.4. Extension of the Archimedean ordered field of real numbers to a non-Archimedean ordered field of complex numbers
The set of hyperreal numbers is a field; its elements have the following properties:
 (11)
(11)
In addition to arithmetic operations on hyperreal numbers, the order is given:
 (12)
(12)
The field in which the order is entered is called the ordered field.
The question of the existence of hyperreal numbers that is a non-Archimedean ordered field of real numbers is formulated as follows [10]: is it possible to construct an extension of the set of real numbers for which the main hypothesis would be satisfied. The main hypothesis requires that:
- here was a set of hyperreal numbers °R for which
![]() ;
;
- for each function f in R, there is a function °f in °R that is an extension of the original function;
- any system of equations and inequalities whose hyperreal analog has (hyper-real) solutions had real solutions;
- R contained infinitesimal elements, other than zero.
In the paper [10] it is shown that under certain conditions these requirements can be met. We assume that the main hypothesis is also satisfied with hypercomplex numbers. Although the property mentioned above of the transition of the actual small to the standard status differs the situation in the hypercomplex numbers from the situation in hyperreal numbers. This fact requires in the strict sense an additional mathematical investigation.
2.5. Differentiation and integration on a non-Archimedean complex number axis
The operations of differentiation and integration are based on the concepts of number, linear space and metric or topological properties of space. The ideology and methods of nonstandard analysis can help to introduce differentiation and integration on a non-Archimedean complex numeric axis.
By now, nonstandard differentiation and integration have been developed. Nonstandard analysis deals with the concepts of derivatives and integrals in a non-standard universe, with standard derivatives and integral defined as standard parts of the corresponding non-standard objects [11]:
 (13)
(13)
Here  (14)
(14)
where R is the field of real numbers. The hyperreal universe is denoted by
 (15)
(15)
where x∈*J—, J— = [a,b]—{b}S is a step function on *J, where J = [a,b].
In the case of a non-Archimedean complex axis, it is necessary to operate in a non-standard universe, without going over to the standard universe at the final stage, as it is done in nonstandard analysis, since it is assumed that the nonstandard universe of a non-Archimedean complex axis is not an ideal, but an actually existing object.
2.6. Investigation of an oscillator on a non-Archimedean complex number axis
In the light of the preceding, let us clarify the results obtained earlier. Let us investigate a second-order linear equation with constant coefficients. By the main hypothesis considered in Section 2.4, we assume that this equation has a solution also on a non-Archimedean complex numerical axis.
Equation
 (16)
(16)
describes a mechanical oscillator and an electric oscillatory circuit. Complex functions are the y-particle displacement, the argument t is the time and parameters: m is the particle mass, ![]() is the friction coefficient, and
is the friction coefficient, and ![]() is the elasticity coefficient. As initial conditions, we take:
is the elasticity coefficient. As initial conditions, we take:
 (17)
(17)
The solution of the Cauchy problem (16), (17) is known:
![]() (18)
(18)
Here k1,2 are the roots of the characteristic equation:
 (19)
(19)
the coefficients c1 and c2 are determined from the initial conditions (17)
 (20)
(20)
It can be seen from formula (19) that three parameters are involved in the determination of the roots of the characteristic equation: m,![]() ,
,![]() . Calculations are carried out for the values of real parts
. Calculations are carried out for the values of real parts ![]()
First, let’s assume that time really is. In Fig. 8 shows the calculated dependence of the real part of the roots (19) of the imaginary parts of the friction coefficient ![]() and the elasticity coefficient
and the elasticity coefficient ![]() at a fixed value of the imaginary part of weight
at a fixed value of the imaginary part of weight ![]() As can be seen everywhere in the domain there are negative values of the coefficients k1,2, which corresponds to the damped oscillations. Fig. 9 shows the time sweep of oscillations and their phase portrait, which is a stable focus. Oscillations are damped slowly because the coefficient of friction is much less than the elastic coefficient. With a value
As can be seen everywhere in the domain there are negative values of the coefficients k1,2, which corresponds to the damped oscillations. Fig. 9 shows the time sweep of oscillations and their phase portrait, which is a stable focus. Oscillations are damped slowly because the coefficient of friction is much less than the elastic coefficient. With a value ![]() , one of the roots k1,2 becomes positive in a certain region of imaginary values of the coefficients of friction and elasticity Im
, one of the roots k1,2 becomes positive in a certain region of imaginary values of the coefficients of friction and elasticity Im![]() and Im
and Im![]() , see Fig. 10. In this region, the oscillations are the beats shown in Fig. 11.
, see Fig. 10. In this region, the oscillations are the beats shown in Fig. 11.
Let us now investigate the question of how the complexity of the time affects the process. Fig. 12 shows the results of the calculation of the oscillations for the imaginary part of the time ![]() . One can be seen that this value of the imaginary part of the time has virtually no effect on the oscillations. However, an increase in the imaginary part of the time up
. One can be seen that this value of the imaginary part of the time has virtually no effect on the oscillations. However, an increase in the imaginary part of the time up ![]() leads to a smoothing of the pulsations and an increase in the amplitude of the oscillations (see Fig. 13). With an increase in the imaginary part of the time, the phase trajectory, which previously filled the interior of the ellipse (see Figs 11, 12), begins to center within a certain torus (see Fig. 13).
leads to a smoothing of the pulsations and an increase in the amplitude of the oscillations (see Fig. 13). With an increase in the imaginary part of the time, the phase trajectory, which previously filled the interior of the ellipse (see Figs 11, 12), begins to center within a certain torus (see Fig. 13).
We can say that the solution of problem (16), (17) in the six-dimensional parameter space {Rem, Imm, Rek, Imk. Re![]() , Im
, Im![]() } is stable (ie, the oscillations are damped) everywhere except for some regions. In these areas, the solution loses stability, that is, the real part of one of the roots (19) becomes positive, and the oscillations increase, despite the dissipation in the system. The imaginary in time, as calculation shows, leads to a smoothing of pulsations, i.e., tends to guide the process to a more stable state.
} is stable (ie, the oscillations are damped) everywhere except for some regions. In these areas, the solution loses stability, that is, the real part of one of the roots (19) becomes positive, and the oscillations increase, despite the dissipation in the system. The imaginary in time, as calculation shows, leads to a smoothing of pulsations, i.e., tends to guide the process to a more stable state.
3. About setting up a test experiment
Thus, a classical mechanical oscillator with the highest possible frequency of ω≈1011 Hz and a minimum friction of ![]() = 0,05 Hz g (these two requirements lead it to the edge of the quantum world) is one of the most suitable experimental systems for carrying out experimental studies to detect the possible complex nature of physical quantities. To ensure such characteristics of the generator, it is necessary to use cryogenic and vacuum equipment [12]. In a series of experiments demonstrating an ordinary, convergent solution (see Figs 8- 9), it is possible to detect a certain number of divergent solutions (beats) (see Figs 10- 13), due to imaginary parts of the coefficients and time.
= 0,05 Hz g (these two requirements lead it to the edge of the quantum world) is one of the most suitable experimental systems for carrying out experimental studies to detect the possible complex nature of physical quantities. To ensure such characteristics of the generator, it is necessary to use cryogenic and vacuum equipment [12]. In a series of experiments demonstrating an ordinary, convergent solution (see Figs 8- 9), it is possible to detect a certain number of divergent solutions (beats) (see Figs 10- 13), due to imaginary parts of the coefficients and time.
4. Conclusion
The first part of the study shows the dual nature of the use of complex numbers in modern physics. Complex numbers ceased to be only an object of mathematical reality and passed into physical reality. However, the dominant ideology still requires that real numbers be put in correspondence with physical quantities. As a result, logical and intellectual dissatisfaction arises.
The second part of the study shows how one can try to build physics in the field of complex numbers. The concept of non-Archimedean complex number axis is introduced. Some effects of complex-valued physics are considered, and methods for experimental verification of the complexness of physical quantities are proposed. We note here that if we take their standard values for the values of the parameters and the initial conditions and construct a solution on the standard values of the argument, we obtain the usual solution of the equation under consideration on the field of real numbers, i.e., damped oscillations in the presence of dissipation in the system. The solution on the non-Archimedean complex numerical axis has completely unusual properties (see Figs 11- 13).
Now in physics, the generalization of complex numbers is intensively used — hypercomplex numbers. Starting with Euler, who proposed a geometric interpretation of complex numbers in the plane and Hamilton, who proposed quaternions for the description of three-dimensional space, hypercomplex numbers are used to create an adequate geometry of space. In order to overcome the difficulties that have entered in physics with the introduction of such objects as «dark matter» and «dark energy,» researches are trying to create a new space-time geometry-Finsler geometry with the Berwald-Moore metric based on quadrics [13, 14, 15, 16, 17]. This geometry is a generalization of Riemannian geometry.
The proposed complexification does not lie in the way of creating geometric models of space by the generalization of complex numbers; it only offers to consider all physical quantities on the field of complex numbers in ordinary three-dimensional Euclidean space.
REFERENCES
1. Lyapunov, A.M. (1956). “General problem of the stability of motion,” Collected Works, Moscow, (in Russian).
2. Lyahov, V.V., Neshchadim, V.M. (2001a). “Complex Numbers and Physical Reality,” arXiv preprint physics/0102047.
3. Lyahov, V.V., Neshchadim, V.M. (2001b). “On Stability of Physics Systems in the Complex Plane,” arXiv preprint physics/0111052.
4. Lyahov, V.V., Neshchadim, V.M. (2018). “Models of Plasma Kinetics and Problems with Their Interpretation in the Current Paradigm,” New York, Nova Science Publishers.
5. Antonov, А.А. (2008). «Physical Reality of Resonance on Complex Frequencies,» European Journal of Scientific Research, 21(4), pp. 627-641.
6. Kline, M. (1988). “Mathematics. Search for Truth”, Moscow, Mir, (in Russian).
7. Kolmogorov, A.I. (1990). “On the Concepts of Quantity and Number,” Collection ”Historical and Mathematical Investigations,” vol. 32-33, Moscow, Nauka, (in Russian).
8. Hilbert, D. (1948). “Foundations of Geometry,” Moscow-Leningrad, State Technical Press, (in Russian).
9. Medvedev, F.A. (1993). “Luzin about non-Archimedean time,” Collection ”Historical and Mathematical Investigations,” vol. 34, Moscow, Nauka, (in Russian).
10. Uspensky V.A.(1987) What is non-standard analysis? Moscow, Nauka, (in Russian).
11. Davis, M. (1980). “Applied Nonstandard Analysis,” Moscow, Mir, (in Russian).
12. Braginsky, V.B., Mitrofanov, V.P., Popov, V.I. (1981). “Systems with Low Dissipation,” Moscow, Nauka, (in Russian).
13. Round, X. (1981). “Differential Geometry of Finsler Spaces,” Moscow, Science, (in Russian).
14. Shen, Z. (2001). “Differential Geometry of Spray and Finsler Spaces,” Dordrecht, Kluwer Academic Publishers.
15. Antonelli, P.L.(2003). “Handbook of Finsler Geometry,” Dordrecht, Kluwer Academic Publishers.
16. Pavlov, D.G. (2010). “About the V International School-seminar «Fundamentals of Finsler Geometry and Its Applications in Physics,” Hypercomplex Numbers in Geometry and Physics, № 2 (14), volume 7, (in Russian).
17. Panchelyuga, V.A. (2010). “Benoit Mandelbrot: the Path to the Fractal Geometry of Nature,” Hypercomplex Numbers in Geometry and Physics, № 2 (14), volume 7, (in Russian).