Vorokhobin I.I.
PhD, associate professor,
National University «Odessa Maritime Academy»
Ворохобин Игорь Игоревич
кандидат технических наук, декан факультета МПиТ,
Национальный университет «Одесская морская академия»
APPLICATION OF MAXIMUM LIKELIHOOD METHOD FOR ESTIMATION OF EFFECTIVE COORDINATES OF SHIP
ПРИМЕНЕНИЕ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ДЛЯ ОЦЕНКИ ЭФФЕКТИВНЫХ КООРДИНАТ СУДНА
Summary: The maximum likelihood method of calculation of coordinates of ship is considered for different laws of distributing of their errors. Analytical expressions of calculation of coordinates of ship are got, providing their maximal exactness.
The imitation design is conducted, the results of which confirmed correctness of analytical expressions of estimation of efficiency of the coordinates expected by a least-squares method at distributing of errors of lines of position on the mixed laws of both types.
Keywords: navigation accident rate, least-squares method, maximum likelihood method, estimation of efficiency of coordinates.
Аннотация:
Рассмотрен метод максимального правдоподобия расчета обсервованных координат судна для различных законов распределения их погрешностей. Получены аналитические выражения расчета обсервованных координат судна, обеспечивающие их максимальную точность.
Проведено имитационное моделирование, результаты которого подтвердили корректность аналитических выражений оценки эффективности обсервованных координат, рассчитанных методом наименьших квадратов при распределении погрешностей линий положения по смешанным законам обоих типов.
Ключевые слова: навигационная аварийность, метод наименьших квадратов, метод максимального правдоподобия, оценка эффективности обсервованных координат.
Постановка проблемы.
Обеспечение надлежащего уровня безопасности судовождения существенно зависит от точности контроля места судна при плавании в стесненных водах. Как показал анализ статистических материалов погрешностей навигационных измерений, в ряде случаев погрешности не подчиняются нормальному закону распределения и в случае избыточных измерений при расчете координат судна по методу наименьших квадратов происходит потеря их точности, чего можно избежать, применяя для расчета координат метод максимального правдоподобия.
Анализ последних достижений и публикаций.
Во многих работах отечественных и зарубежных ученых освещены вопросы повышения точности определения места судна. Результаты анализа статистических материалов точности определения места судна с помощью приёмника спутниковой радионавигационной системы представлены в работе [1], которые показали, что предположение о распределении случайных погрешностей определения широты и долготы по закону Гаусса не является корректным и требует альтернативного подхода.
В работах [2, 3] рассматриваются вопросы законов распределения вероятностей погрешностей навигационной измерений исходной выборки, которая является смесью частных выборок нормально распределенных погрешностей с разной дисперсией. Предложена процедура оценки эффективности обсервованных координат судна с учетом смешанных распределений погрешностей исходной выборки.
В работах [4, 5] представлен анализ статистических данных погрешностей навигационных измерений, полученных в натурных наблюдениях, который показал, что погрешности навигационных измерений не подчиняются нормальному закону распределения.
Анализ выборок случайных погрешностей измерений навигационных параметров произведен в работе [6] и показано, что наибольшее согласие статистического материала с теоретическим распределением достигается для законов, отличающихся от нормального закона.
В этом случае, как указано в работах [7, 8], применение метода наименьших квадратов для расчета обсервованных координат судна не обеспечивает возможности получения их эффективных оценок. Поэтому для получения эффективных оценок обсервованных координат судна следует использовать метод максимального правдоподобия, учитывающий действительный закон распределения погрешностей. Данное обстоятельство в настоящее время не учитывается, и соответствующие аналитические выражения получения эффективных оценок отсутствуют.
Выделение нерешенных ранее частей общей проблемы.
Как показывает анализ рассмотренных работ, при избыточных измерениях навигационных параметров расчет обсервованных координат следует производить методом максимального правдоподобия с учетом закона распределения вероятностей случайных погрешностей измерения, чем достигается максимальная точность определяемых координат. При этом необходимо располагать алгоритмом расчета координат судна с учетом закона распределения вероятностей случайных погрешностей измерения навигационных параметров, формирование которых является предметом исследования данной статьи.
Цель статьи.
Целью статьи является разработка аналитических выражений расчета координат судна при наличии избыточных измерениях навигационных параметров методом максимального правдоподобия, который учитывает закон распределения вероятностей погрешностей навигационных измерений.
Изложение основного материала.
Основной мерой повышения точности определения обсервованных координат судна является использование избыточных линий положения [4], учет которых производится методом максимального правдоподобия. Как указывается в работе [9], система уравнений правдоподобия имеет следующий вид:


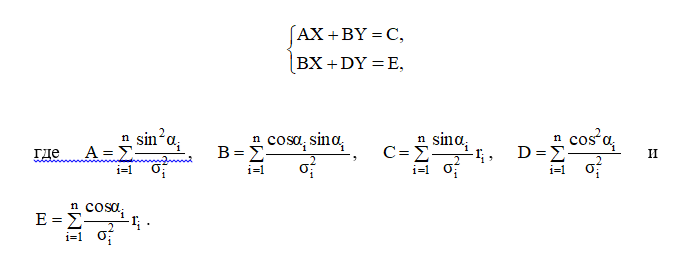
Решая последнюю систему уравнений, получим значения X и Y, являющиеся эффективными оценками приращений счислимых координат,

Поэтому:
 .
.

Получили уравнение, в левой части которого находится переменная X.
Аналогично, со второго уравнения системы (3) находим выражение для второй неизвестной переменной Y:

Рассмотрим применение метода максимального правдоподобия для расчета обсервованных координат судна при распределении погрешностей линий положения по обобщенному закону Пуассона. Для реализации метода максимального правдоподобия необходимо составить функцию правдоподобия, используя выражение для плотности [11]:
 где , .
где , .
Система уравнений правдоподобия для рассматриваемого случая принимает
следующий вид:
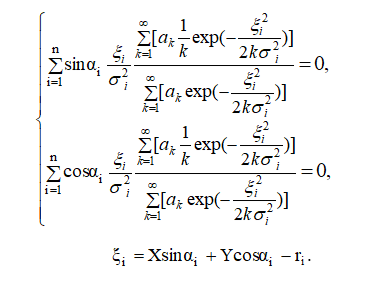
Рассмотрим решение полученной нелинейной системы уравнений методом простой итерации. Первое уравнение можно записать в следующем виде:
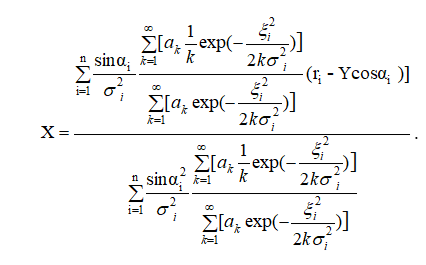
Получили уравнение, в левой части которого находится искомая переменная X. Аналогично, со второго уравнения системы находим выражение для второй неизвестной переменной Y:
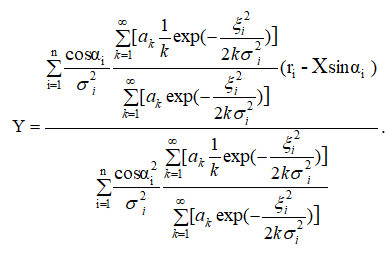

приближения искомых переменных, которые являются исходными для очередной итерации. Расчет обсервованных координат по избыточным линиям положения, погрешности которых подчиняются обобщенному закону Пуассона, с помощью предлагаемого алгоритма обеспечивает минимальную ковариационную матрицу векториальной погрешности.
Для оценки эффективности обсервованных координат, полученных при избыточных ЛП и рассчитанных методом наименьших квадратов проводилось имитационное компьютерное моделирование [9]. Причем рассматривались случаи, когда погрешности линий положения подчинялись нормальному закону, а также смешанным законам первого и второго типа.
Имитационное моделирование проводилось по следующему алгоритму. Вначале по выбранному закону распределения генерировалась выборка погрешностей
 состоящая из 1000 обсервованных точек, приращения координат X и Y которых являются проекциями векториальной погрешности, позволяющим рассчитать ковариационную матрицу векториальной погрешности обсервации. Формирование 125 обсервованных точек повторялось четыре раза, а их полученные координаты сохранялись, в результате чего накапливалась
состоящая из 1000 обсервованных точек, приращения координат X и Y которых являются проекциями векториальной погрешности, позволяющим рассчитать ковариационную матрицу векториальной погрешности обсервации. Формирование 125 обсервованных точек повторялось четыре раза, а их полученные координаты сохранялись, в результате чего накапливалась
 координат векториальной погрешности. Имитационной компьютерной программой предусмотрено графическое отображение положений обсервованных точек относительно математического ожидания, что позволяет произвести визуальную оценку их рассеяния. Учитывая, что векториальная погрешность определяется относительно истинного места судна, при имитационном моделировании для оценки эффективности обсервованных координат необходимо использовать не дисперсии проекций X и Y, а их вторые начальные моменты.
координат векториальной погрешности. Имитационной компьютерной программой предусмотрено графическое отображение положений обсервованных точек относительно математического ожидания, что позволяет произвести визуальную оценку их рассеяния. Учитывая, что векториальная погрешность определяется относительно истинного места судна, при имитационном моделировании для оценки эффективности обсервованных координат необходимо использовать не дисперсии проекций X и Y, а их вторые начальные моменты.
В компьютерной программе имитационного моделирования предусмотрен расчет обсервованных координат, как методом наименьших квадратов, так и методом максимального правдоподобия. При имитационном

Для оценки эффективности обсервованных координат судна рассчитанных методом наименьших квадратов, погрешности линий положения которых подчиняются смешанным распределениям, генерировались выборки погрешностей ЛП по смешанному закону, а затем рассчитывались обсервованные координаты методом наименьших квадратов


Сравнительная характеристика рассеяния обсервованных точек, координаты которых рассчитаны МНК и ММП, представлена на рис. 1.
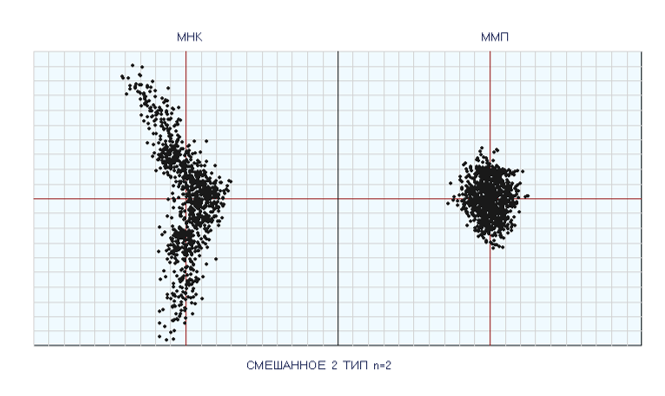
Рис. 1. Рассеяние обсервованных точек при m=2.
Таким образом, результаты имитационного моделирования подтвердили корректность аналитических выражений оценки эффективности обсервованных координат, рассчитанных методом наименьших квадратов при распределении погрешностей линий положения по смешанным законам обоих типов.
Выводы и предложения.
1. Рассмотрен метод максимального правдоподобия расчета обсервованных координат судна при наличии избыточных линий положения для различных законов распределения их погрешностей.
2. Получены аналитические выражения расчета обсервованных координат судна, обеспечивающие их максимальную точность.
3. Проведено имитационное моделирование, результаты которого подтвердили корректность аналитических выражений оценки эффективности обсервованных координат, рассчитанных методом наименьших квадратов при распределении погрешностей линий положения по смешанным законам обоих типов.
Список литературы:
1. Monteiro Luis. What is the accuracy of DGPS? / Sardinia Monteiro Luis, Moore Terry, Hill Chris. // J. Navig. 2005. 58, № 2, p. 207-225.
2. Астайкин Д.В. Оценка точности позиции судна при наличии случайных погрешностей навигационных измерений / Астайкин Д.В. // Проблеми техніки: Науково-виробничий журнал. — 2014. № 4 . – С. 147-152.
3. Астайкин Д.В. Аналитическое выражение функции распределения случайных величин смешанных законов/ Астайкин Д.В. // Водный транспорт. – 2014. №2 (20).– С. 6 – 11.
4. Кондрашихин В.Т. Определение места судна / Кондрашихин В.Т. — М.: Транспорт, 1989. — 230с.
5. Hsu D. A. An analysis of error distribution in navigation / Hsu D. A. // The Journal of Navigation. – Vol. 32.- № 3. – P. 426 — 429.
6. Мельник Е.Ф. Приближенное описание смешанных распределений погрешностей навигационных измерений / Мельник Е.Ф. // Автоматизация судовых технических средств: науч. –техн. сб. – 2002. – Вып. 7.- Одесса: ОГМА. – С. 96 – 100.
7. Мудров В.М. Методы обработки измерений / Мудров В.М., Кушко В.Л. — М.: Советское радио, 1976. 192 с.
8. В.В. Степаненко. Эффективность оценки параметров ситуации опасного сближения судов/ В.В. Степаненко. // Судовождение: Сб. науч. трудов / ОГМА. – Вып. 2 – Одесса: Латстар, 2000. – С. 201 – 209.
9. Астайкин Д.В. Оценка точности координат судна при избыточных измерениях/ Астайкин Д.В., Сикирин В.Е., Ворохобин И.И., Алексейчук Б.М. – Saarbrucken, Deutschland/Германия: LAP LAMBERT Academic Publishing, 2017. – 274 с.
10. Турчак Л. И. Основы численных методов/ Турчак Л. И. – М.: Наука. Гл. ред. физ. – мат. лит., 1987. – 320 с.
11. Сикирин В.Е. Описание навигационных погрешностей с помощью обобщенного распределения Пуассона/ Сикирин В.Е.// Судовождение: Сб. научн. трудов./ОНМА, Вып. 26. – Одесса: «ИздатИнформ», 2016 — С. 152 – 156.