В. М. КОФМАН

МЕТОД ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ГТД НА УСТАНОВИВШИХСЯ РЕЖИМАХ РАБОТЫ

V.M. KOFMAN

PARAMETRIC IDENTIFICATION METHOD OF THE GAS TURBINE ENGINE MATHEMATICAL MODELS ON THE DETERMINED WORK MODES

There has been carried out the analysis of the existing parametric identification mathematical models methods of the gas turbine engine on the determined work modes. There has been offered a new identification method. The method has been developed on the basis of the synthesis of the traditional method and one of the formalized methods (the least square method) and on condition of preserving the advantages of these methods it eliminates the limitations they possess. In the least square method there have been considered the correlations between the unknowns what allows to reduce substantially the number of the unknowns in the identification task and to increase the physical meaning of the task received. The method has been tested while carrying out numerical experiments and identifying the mathematical model of the designed gas turbine engine according to the results of the bench test. Gas turbine engine; mathematical model; identification.

Аннотация

Проведен анализ существующих методов параметрической идентификации математических моделей газотурбинных двигателей на установившихся режимах работы. Предложен новый метод идентификации. Метод разработан на основе синтеза традиционного метода и одного из формализованных методов (метода наименьших квадратов) и при сохранении достоинств этих методов устраняет присущие им ограничения. В предлагаемом методе учтены корреляционные связи между неизвестными, что позволяет существенно уменьшить количество неизвестных в задаче идентификации и повысить физический смысл получаемого решения. Метод апробирован при проведении численных экспериментов и при идентификации математической модели выполненного ГТД по результатам его стендовых испытаний. ГТД; математическая модель; идентификация.

ВВЕДЕНИЕ

Одним из важных инструментов, применяемых на всех этапах проектирования, доводки и серийного производства газотурбинного двигателя (ГТД), является его математическая модель (ММ) на установившихся режимах. ММ ГТД позволяет проводить расчеты высотно-скоростных характеристик ГТД, формировать исходные данные для газодинамических расчетов и проектирования узлов ГТД, проектирования системы автоматического управления ГТД, проведения расчетов температурного состояния деталей и расчетов на прочность, планирования различных видов испытаний, диагностики состояния ГТД в процессе эксплуатации. Эффективность применения ММ ГТД зависит от ее точности. Процесс повышения точности ММ ГТД на установившихся режимах за счет структурной идентификации ММ (введения в структуру ММ дополнительных уравнений, учитывающих физические особенности рабочего процесса ГТД более высокого порядка) близок к своему завершению. Поэтому на первый план выходит задача повышения точности ММ ГТД за счет параметрической идентификации (ПИ) – задача уточнения по результатам испытаний ГТД характеристик его узлов. В данной работе описан метод идентификации, разработанный на основе традиционного метода увязки и одного из формализованных методов идентификации (метода наименьших квадратов). Разработанный метод при сохранении достоинств существующих методов идентификации устраняет присущие им ограничения.

1. АНАЛИЗ СУЩЕСТВУЮЩИХ МЕТОДОВ ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ГТД НА УСТАНОВИВШИХСЯ РЕЖИМАХ РАБОТЫ

Одной из первых работ по ПИ ММ ГТД является метод так называемой традиционной увязки ММ ГТД с результатами его испытаний (Б. Н. Амелин,

О. Н. Фаворский, ЦИАМ, 1955 г.). Идентификация ММ в традиционном методе увязки осуществляется путем решения двух термогазодинамических задач – прямой и обратной. При решении обратной задачи по результатам эксперимента определяются характеристики узлов ГТД. При решении прямой задачи до и после идентификации производится оценка адекватности ММ ГТД реальному двигателю путем сравнения величин расчетных параметров ГТД с величинами экспериментально измеренных параметров. Сущность идентификации ММ ГТД при методе традиционной увязки состоит в решении обратной термогазодинамической задачи (решении для каждой, полученной при испытаниях ГТД экспериментальной точки, системы определяющих (нелинейных алгебраических) уравнений, описывающих физические процессы, происходящие в ГТД).

Количество неизвестных в системе определяющих уравнений в обратной задаче зависит от сложности схемы ГТД и от степени препарирования проточной части ГТД при проведении его испытаний. Система определяющих уравнений в общем виде имеет вид

минимума некоторой выбранной функции цели, как правило, минимума суммы квадратов невязок между экспериментально измеренными и расчетными параметрами ГТД. Поиск решения при идентификации в [1, 2] производится одновременно для всех экспериментальных точек. В [3, 4, 5, 6] поиск решения производится сначала для каждой отдельной экспериментальной точки с последующим заключительным, например, многомерным регрессионным анализом, при котором уточняются характеристики узлов по результатам идентификации для каждой экспериментальной точки [4, 5], либо с помощью какого-либо другого вида анализа [6], при котором рассматриваются несколько вариантов решения (вариантов математической модели ГТД) и выбирается один из них. Например, в методе наименьших квадратов [1] функция цели имеет вид

Достоинством формализованных методов [1, 2] является их достаточно высокая эффективность с позиций обеспечения сходимости между расчетными и экспериментально измеренными при испытаниях параметрами ГТД в различных условиях и на различных режимах. Методы [3–6] являются менее эффективными, так как после проведения идентификации в каждой из экспериментальных точек необходимо проводить многомерный регрессионный анализ для получения сведений о характере изменения параметров характеристик узлов. Характеристики узлов ГТД являются в общем случае функциями или двух переменных (камера сгорания, реактивное сопло), или трех переменных (компрессор, турбина), а сами величины переменных (критериев подобия или безразмерных параметров), определяющих режим работы узла, в каждой экспериментальной точке различны. Поэтому для получения обобщенных характеристик узлов на основе результатов идентификации в отдельных экспериментальных точках требуются не только известные методы математической статистики, но и разработка специальных методик обработки и анализа.

2. МЕТОД ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ГТД .

ОСНОВНЫЕ ПОЛОЖЕНИЯ, УРАВНЕНИЯ И СТРУКТУРНАЯ СХЕМА

Учитывая достоинства и ограничения существующих методов ПИ ММ ГТД, была поставлена задача разработать метод ПИ ММ ГТД, который, являясь развитием традиционного метода увязки и формализованного метода идентификации [1], позволял бы по результатам эксперимента более физически обоснованно определять параметры (коэффициенты) характеристик узлов ГТД при обеспечении хорошей адекватности уточняемой ММ ГТД реальному объекту.

Логические предпосылки построения такого метода параметрической идентификации ММ ГТД вытекают из следующих рассуждений.

Пусть при испытаниях ГТД измерено его выходных параметров в экспериментальных точках на различных режимах работы. Имеется соответствующая типу ГТД и его схеме система определяющих (нелинейных алгебраических) уравнений, описывающих физические процессы, происходящие в ГТД. Построим на основе системы определяющих уравнений две задачи.

измерений. Принцип решения такой системы предложен Лежандром [9], и состоит он в следующем. Если дана система равноточных условных уравнений и если измерения независимы, ошибки измерений подчиняются нормальному закону распределения, ошибка расчета мала по сравнению с ошибками измерений, то наиболее вероятные значения неизвестных определятся из условия минимума суммы квадратов невязок.

Для системы (6) это условие соответствует минимуму функции цели

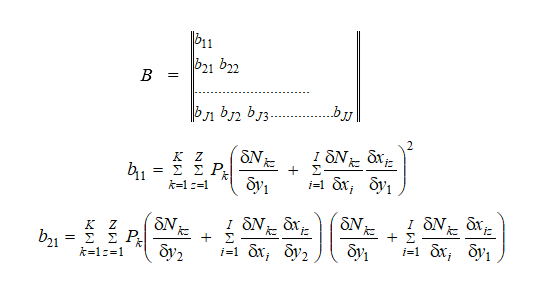
которые имеют большие коэффициенты взаимной корреляции [1]. Получение устойчивого решения также возможно за счет применения прямых методов естественной регуляризации обратной задачи путем изменения параметров вычислительного алгоритма (шагов по аргументам, количества итераций) [15]. Способ обеспечения корректной постановки обратной задачи выбирается в каждом конкретном случае индивидуально в зависимости от физической стороны решаемой задачи. Схема разработанного метода параметрической идентификации приведена на рис.1.

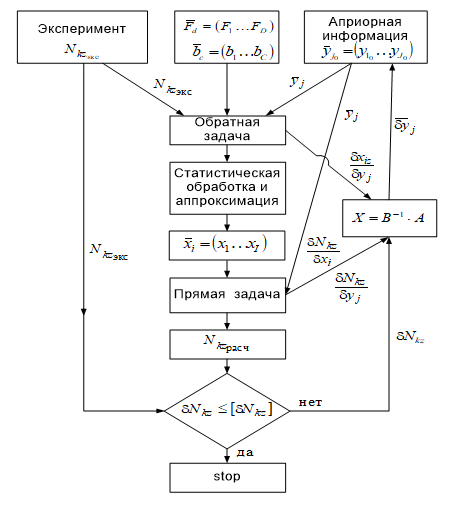
Рис. 1. Схема метода параметрической идентификации ММ ГТД

3. АПРОБАЦИЯ МЕТОДА ИДЕНТИФИКАЦИИ

Разработанный метод был апробирован при идентификации ММ выполненного одновального ГТД по результатам его испытаний на наземном и высотном стендах в широком диапазоне эксплуатационных условий. Применительно к этому ГТД были разработаны методики и соответствующие программы решения прямой и обратной термогазодинамических задач. Также была разработана методика и программа «OPTIMA 1» решения системы нормальных уравнений вида (9) (задача оптимизации), не зависящая от типа и схемы ГТД. Программы составлены на языке программирования Compaq Visual Fortran Version 6.6.

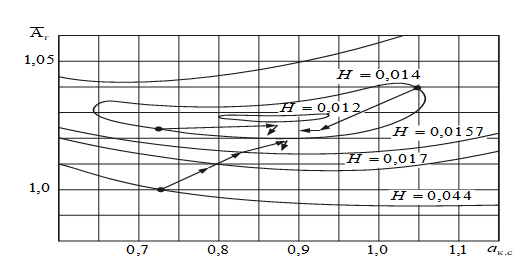
Рис. 2. Результаты поиска решения при идентификации ММ ГТД

После проведения идентификации и поверочного расчета по прямой задаче с помощью уточненной ММ ГТД средние абсолютные величины невязок по таким параметрам как тяга, расход топлива, полное давление за компрессором и полное давление за турбиной в исследуемом эксплуатационном диапазоне работы ГТД уменьшились в 2…3 раза –

с 1,6..3,6 % до 0,6..1,2 %). В меньшей степени изменились невязки по таким параметрам как расход воздуха через ГТД и заторможенная температура воздуха за компрессором, средние величины невязок по которым после идентификации составили соответственно 1,5 % и 0,3 %.

ВЫВОДЫ

1. Разработан метод параметрической идентификации ММ ГТД на установившихся режимах работы, который, по сравнению с существующими формализованными методами, позволяет (за счет введения в процедуру идентификации обратной термогазодинамической задачи и учета при решении задачи идентификации корреляционных связей между уточняемыми коэффициентами характеристик узлов ГТД) сократить количество неизвестных коэффициентов (параметров характеристик узлов), определяемых при решении задачи оптимизации, уточнять характеристики узлов ГТД в нелинейной постановке как функции нескольких переменных, повысить физическую обоснованность получаемых решений.

2. Метод имеет высокую эффективность с позиций обеспечения после идентификации сходимости между расчетными и экспериментально измеренными параметрами ГТД. Метод базируется на использовании ММ обратной и прямой ТГЗ и задачи оптимизации. Входящая в разработанный метод ПИ задача оптимизации является общей для всех типов и схем ГТД.

СПИСОК ЛИТЕРАТУРЫ

1. Тунаков, А. П. Методы оптимизации при доводке и проектировании газотурбинных двигателей / А. П. Тунаков. М.: Машиностроение, 1979. 184 с.

2. Ахмедзянов, А. М. Согласование моделей ТРД с результатами эксперимента при ограниченном его объеме / А. М. Ахмедзянов, Х. С. Гумеров, Е. И. Марковникова, Ю. Д. Дегтярев // Испытания авиационных двигателей : Межвуз. науч. сб. Уфа : 1978. № 6. С. 13-19.

3. Курлыков, В. А. Идентификация математических моделей авиационных ГТД с использованием методов нелинейной оптимизации / В. А. Курлыков, А. М. Ахмедзянов // Испытания авиационных двигателей : Межвуз. науч. сб. Уфа : 1979. № 7. С. 85-89.

4. Боровик, В. О. Анализ результатов испытаний ГТД с использованием математических моделей и методов математической статистики / В. О. Боровик, Е. М. Таран // Испытания авиационных двигателей : Межвуз. науч. сб. Уфа : 1978. № 6. С. 3-12.

5. Литвинов, Ю. А. Характеристики и эксплуатационные свойства авиационных турбореактивных двигателей / Ю. А. Литвинов, В. О. Боровик. М.: Машиностроение, 1979. 288 с.

6. Бочкарев, С. К. Опыт и проблемы компьютеризированного термогазодинамического анализа результатов испытаний газотурбинных двигателей сложных схем / С. К. Бочкарев, А. Я. Дмитриев, В. В. Кулагин и др. // Изв. вузов. Авиационная техника, 1993. № 2. С. 68-70.

7. Хусточка, А. Н. Применение теории нечетких множеств при идентификации математических моделей ГТД / А. Н. Хусточка // Вестник двигателестроения : науч. техн. журн. Запорожье : 2004. № 2. С. 96-99.

8. Тихонов, А. Н. Методы решения некорректных задач / А. Н. Тихонов, В. Я. Арсенин. М.: Наука, 1979. 288 с.

9. Щиголев, Б. М. Математическая обработка наблюдений / Б. М. Щиголев. М.: Наука, 1969. 344 с.

10. Кофман, В. М. Методика уточнения характеристик узлов ГТД по результатам испытаний / В. М. Кофман // Измерение, обработка и анализ информации при доводке, серийном производстве и эксплуатации авиационных ГТД: тез. докл. межотрасл. конф. М.: ЦИАМ, 1979. С. 26-29.

11. Kofman, V. M. Method of parametric identification of mathematical models of gas- turbine engines / V. M. Kofman // Inverse Problems: Identification, Design and Control : Transactions of the 5 International conference. М.: 2007. 10 p.

12. Кофман, В. М. Метод параметрической идентификации математических моделей газотурбинных двигателей / В. М. Кофман // Аэрокосмическая техника и высокие технологиии–2007. Труды Х Всероссийской научно-технической конф. Пермь. 2007. С.147-148.

13. Кофман, В. М. Метод параметрической идентификации математических моделей газотурбинных двигателей / В. М. Кофман // Наука и технологии: тез. докл. ХХVIII Российской школы, Миасс.: 2008. С 49-51.

14. Кофман, В. М. Метод параметрической идентификации математических моделей газотурбинных двигателей / В. М. Кофман // Наука и технологии. Труды ХХVIII Российской школы. Том 2. М.: РАН 2008. С 72-84.

15. Алифанов, О. М. Идентификация процессов теплообмена летательных аппаратов / О. М. Алифанов. М.: Машиностроение, 1979. 216 с.

16. ОСТ 1 01021-93 Стенды испытательные авиационных газотурбинных двигателей. Общие требования. 18 с.