Физико-математические науки
Айтенова Г.М.
PhD студент
Актюбинский региональный государственный университет
имени К.Жубанова
Абдикаликова Г.А.
кандидат физико-математических наук, доцент
доцент кафедры математики
Актюбинский региональный государственный университет
имени К.Жубанова
Сартабанов Ж.А.
доктор физико-математических наук, профессор
профессор кафедры математики
Актюбинский региональный государственный университет
имени К.Жубанова
СУЩЕСТВОВАНИЕ МНОГОПЕРИОДИЧЕСКОГО РЕШЕНИЯ ОДНОЙ СИСТЕМЫ ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
EXISTENCE OF THE MULTIPERIODICAL SOLUTION
OF ONE SYSTEM THE INTEGRAL-DIFFERENTIAL EQUATIONS
Aitenova G.M.
PhD student
K.Zhubanov Aktobe Regional State University
Abdikalikova G.A.
Candidate of Physical and Mathematical Sciences,
Associate Professor of Department Mathematics
K.Zhubanov Aktobe Regional State University
Sartabanov Zh.A.
Doctor of Physical and Mathematical Sciences,
Professor of the Department Mathematics
K.Zhubanov Aktobe Regional State University
Аннотация: Исследуется система интегро-дифференциальных уравнений типа Вольтерра с оператором дифференцирования по направлениям векторного поля. Построен матрицант удовлетворяющий матричному уравнению и получены некоторые её свойства и оценки, связанные с многопериодичностью по временным переменным. Установлены достаточные условия существования и единственности многопериодического по всем независимым переменным решения системы интегро-дифференциальных уравнений.
Abstract: Researched the system of Volterra type integro-differential equations with the differentiation operator by directions of the vector field. Constructed the matricant satisfies the matrix equation and obtained some of its properties and estimates that are related to multiperiodical in time variables. Established sufficient conditions the existence and uniqueness of the multiperiodical in all independent variables of the solution system integro-differential equations
Ключевые слова: матрицант, многопериодичность, резольвента, ядро, Коши, Грин.
Keywords: matricant, multiperiodical, resolvent, kernel, Cauchy, Green.
Постановка проблемы. Рассмотрим интегро-дифференциальное уравнение


Анализ исследований и публикаций. Интегро-дифференциальные уравнения возникают во многих разделах прикладной математики. Как известно, исследованием теории интегро-дифференциальных уравнений занимались многие авторы. Проблемам теории периодических и почти периодических колебаний, условиям существования ограниченных, почти периодических и периодических решений посвящены работы многих авторов, отметим [1-3]. В [4] рассмотрены распространение результатов М.Урабе на системы интегро-дифференциальных уравнений, исследованы представления решения интегро-дифференциальных уравнений через резольвенту ядра [5], указана роль этих уравнений при описаний процессов с последействиями [6], применение их в математической биологии [7]. Исследования почти периодических решений систем уравнений с квазипериодическими правыми частями [8], почти периодических решений интегро-дифференциальных уравнений типа переноса [9-10], существование и построение многопериодических и псевдопериодических решений систем интегро-дифференциальных уравнений, содержащих пространственную переменную рассмотрены в [11].
Постановка задачи. Цель настоящей работы – установить достаточные условия существования и единственности многопериодического решения системы интегро-дифференциального уравнения (1).

из уравнения соответствующего неоднородному интегро-дифференциальному уравнению (1) имеем
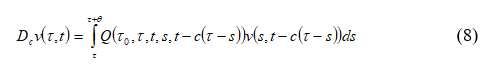






Полученный результат сформулируем в виде теоремы.

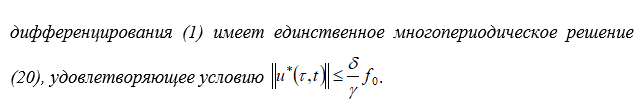
Выводы и перспективы. Для системы интегро-дифференциальных уравнений в частных производных с оператором дифференцирования по направлениям векторного поля, не содержащих пространственных переменных построен матрицант удовлетворяющий матричному уравнению.
Найдены представимость многопериодического решения рассматриваемой интегро-дифференциальной системы через резольвенту ядра, получены рекуррентные соотношения и оценки. Установлены достаточные условия существования и единственности многопериодического по всем независимым переменным решения системы интегро-дифференциальных уравнений. Заметим, что доказанная теорема остается справедливой, когда матричная функция Грина линейной системы обладает свойством экспоненциальной дихотомичностью.
Список литературы:
1. Быков Я.В. О некоторых задачах теории интегро-дифференциальных уравнений. -Фрунзе: Киргиз. гос. ун-т., 1957. — 328 c.
2. Massera I.L. Linear differential equations and functional analysis /I.L.Massera, I.I.Schaffer //I. Annals of math. -1958. -67, -№3. -Pp.517-573.
3. Langenhop C.E. Note on Almost Periodic solutions of Nonlinear Differential Equations /C.E.Langenhop //Jour. Math. Phys., -1959. -38. Pp. 126-129.
4. Самойленко А.М. Метод Бубнова-Галеркина построения периодических решений интегро-дифференциальных уравнений типа Вольтера /А.М.Самойленко, О.Д.Нуржанов //Диффренц. уравнения. -1979. -15, -№8. -C.1503-1517.
5. Барбашин Е.А. Введение в теорию устойчивости. М.: Наука, 1967. -224 c.
6. Иманалиев М.И. Нелинейные интегро-дифференциальные уравнения с частными производными. -Бишкек: Илим, 1992. -112 c.
7. Нахушев А.М. Уравнения математической биологии. -М.: Высшая школа, 1995. -301 c.
8. Харасахал В.Х. Почти периодические решения обыкновенных дифференциальных уравнений. -Алма-Ата: Наука, 1970. -200 c.
9. Умбетжанов Д.У. Почти периодические решения эволюционных уравнений. -Алма-Ата: Наука, 1990. -184 c.
10. Умбетжанов Д.У. О существовании почти многопериодического решения одной системы интегро-дифференциальных уравнений в частных производных /Д.У.Умбетжанов, А.Б.Бержанов //Изв. АН КазССР. Сер. физ.-мат. -1983. -№5. -C.11-15.
11. Сартабанов Ж.А. Псевдопериодические решения одной системы интегро-дифференциальных уравнений /Ж.А. Сартабанов //Укр.математ. журнал. -1989. -41, -№1. -C.125-130.