Using the results of average oscillating velocities for determining the porosity of carboniferous deposits at Dniprovo-Donetska depression

Fedoriv V.V.

candidate of geological science, associate professor of the department of oil and gas geophysics

Ivano-Frankivsk National Technical University of Oil and Gas,

Kashuba G.O.

candidate of geological science

Public Company «Ukrgasvydobuvannia»,

Piatkovska I.O.

candidate of geological science

Ivano-Frankivsk National Technical University of Oil and Gas,

Using the results of average oscillating velocities for determining the porosity of carboniferous deposits at Dniprovo-Donetska depression

Annotation

When calculating the porosity coefficient, the data obtained from the core studies are usually taken into account, but other indicators are not consider. Therefore, taken into account the influence of fluid fluctuations and its hydrodynamic state on magnitude of average oscillatory velocity longitudinal wave will considerably improve quality of determination porosity coefficient.

Keyword words: the coefficient of porosity, the longitudinal velocity, interval time.

Actuality. Coefficient of rock porosity is one of the main parameters, which is determined by the results of geophysical well logging. In works [1,2,4,6,7,8], the following algorithm is proposed which associates the general and effective porosity with other parameters of environment and oscillatory velocities of particles in the longitudinal wave:

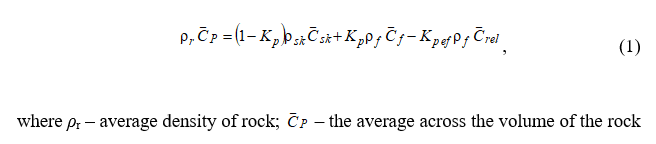
it is possible to obtain from the equation (1) an analogue of the equation for mean time using the values of density and oscillatory velocity of longitudinal and transverse waves:

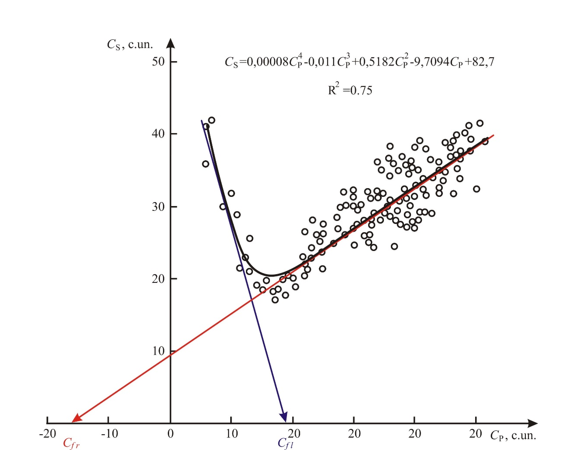
Figure 1 — The nature of change average oscillating velocity of transverse wave, depending on the average oscillatory velocity of longitudinal wave

Figure 2 — Correlation of porosity coefficients determined by the core and average oscillatory velocity of longitudinal wave

Conclusions. Summarizing the above, we can conclude that the methodical approach to determining the coefficient of reservoir rock porosity with the help of data about magnitude oscillatory velocities is sufficiently effective and can be used for gas and gas-condensate fields such as the Dniprovo-Donetska depression and Precarpathian foredeep.

Literature

1. Kratkoe metodicheskoe rukovodstvo po interpretatsyi datyh dinamicheskogo karotaja. VNIIGeofiiki, 1986.
2. Ivakin B.N., Karus E.V., Kuznetsov O.L. Akusticheskyi metod isledovaniia skvajyn. — M.: Nedra, 1978. — 320 p.
3. Willie M.R.J., Gregory A.R., Gardner L.W. Elastic wave velocities in heterogeneous and porous media // Geophysics. – 1956. – V. 21, № 1. – P. 41 – 70.
4. Methods and apparaturs for acoustic logging through casing. [Schlumberger Technology Corp.]: Pat. kl. 340 – 15.5 ВН, (G01V1/40), № 3909775 USA/ Lavigne J.C.; Decl. 26.10.73, № 409.788; Publ. 30.09.75.
5. Raymer L.L., Hunt E.R., Gardner J.S. An improved sonic transit time — toporosity transform // SPWLA 21^st Annual Logging Symposium. 1980, July 8 — 11.
6. Kreif M., Garat J., Stellingwerf J., Ventre J. A petrophysical interpretation the velocities of P and S wave (full- wavtform sonic) // 12th International Formation Evaluation Symposium. – 1989, October 24.
7. Biot M.А. Theory of propagation of clastic waves in a fluid – saturated porovs solid. Part I – II. j. Acoust. SOS. Amer. – 1956. –28. –P. 168 – 175.
8. Halliburton Logging Services Chart Book / 1991, Halliburton publication.
9. Heysses D.R. Sonic poroste transforms and effects of pore shale and clay distribution // Halliburton Energy Services. Х1078. – 1995. – P. 1 — 13.

Fedoriv V.V.

candidate of geological science, associate professor of the department of oil and gas geophysics

Ivano-Frankivsk National Technical University of Oil and Gas,

Kashuba G.O.

candidate of geological science

Public Company «Ukrgasvydobuvannia»,

Piatkovska I.O.

candidate of geological science

Ivano-Frankivsk National Technical University of Oil and Gas,

Using the results of average oscillating velocities for determining the porosity of carboniferous deposits at Dniprovo-Donetska depression

Annotation

When calculating the porosity coefficient, the data obtained from the core studies are usually taken into account, but other indicators are not consider. Therefore, taken into account the influence of fluid fluctuations and its hydrodynamic state on magnitude of average oscillatory velocity longitudinal wave will considerably improve quality of determination porosity coefficient.

Keyword words: the coefficient of porosity, the longitudinal velocity, interval time.

Actuality. Coefficient of rock porosity is one of the main parameters, which is determined by the results of geophysical well logging. In works [1,2,4,6,7,8], the following algorithm is proposed which associates the general and effective porosity with other parameters of environment and oscillatory velocities of particles in the longitudinal wave:

, (1)

where ρ_r – average density of rock; – the average across the volume of the rock oscillating velocity of particles in a longitudinal wave; K_p – coefficient of total porosity; ρ_sk – skeletal rock density;   – oscillatory velocity of longitudinal wave in rock skeleton; ρ_f and  – respectively, the density and oscillating speed for fluid; K_p ef – coefficient of effective porosity;  – velocity of relative displacement the skeleton particles and the fluid that saturates it.

Given such a connection:

(2)

it is possible to obtain from the equation (1) an analogue of the equation for mean time using the values of density and oscillatory velocity of longitudinal and transverse waves:

. (3)

Analysis of published works. According to the authors [3,5,8,9] and own studies, the range of change in value, depending on the change in porosity and hydrodynamic state of the fluid, is an order higher than the interval time of passing longitudinal wave.

To determine the oscillatory velocity of longitudinal wave in porous fluid, compare the concept of interval time propagation of the elastic wave in the fluid ΔT_f and average oscillatory velocity of longitudinal wave in porous fluid.

In papers [7, 8] it was noted that the value of interval time propagation of longitudinal wave in a fluid ΔT_f depends on the composition of the fluid, reservoir temperatures and pressures, and mineralization of the reservoir water.

The purpose of this article. For calculating the coefficient of porosity, develop a mechanism for taking into account the magnitude of oscillating velocities, which will improve the accuracy for determination this coefficient.

Methods of solving the set task. Now let’s pay attention to, since determining this parameter is our main task.

In work [5,6,9] it is shown that with increasing porosity and, consequently, permeability, the oscillating velocity in the time domain of longitudinal wave increases (amplitude). Now let’s pay attention to the behavior of the transverse wave in porous environments. To this end, we will compare the values of the oscillating velocities of longitudinal and transverse waves.

If we construct the above proposed dependence, and the transverse wave does not propagate in fluid media, that is , then continuing the regression line obtained by averaging the points to the intersection of the axis we receive nothing other than.

We have taken data on oscillating velocities and for reservoir rocks of carboniferous deposits at Dniprovo-Donetska depression, the porosity coefficient of which, according to core data, varies from 12 to 28%.As a result, we get the dependence, , which is shown in Fig.1

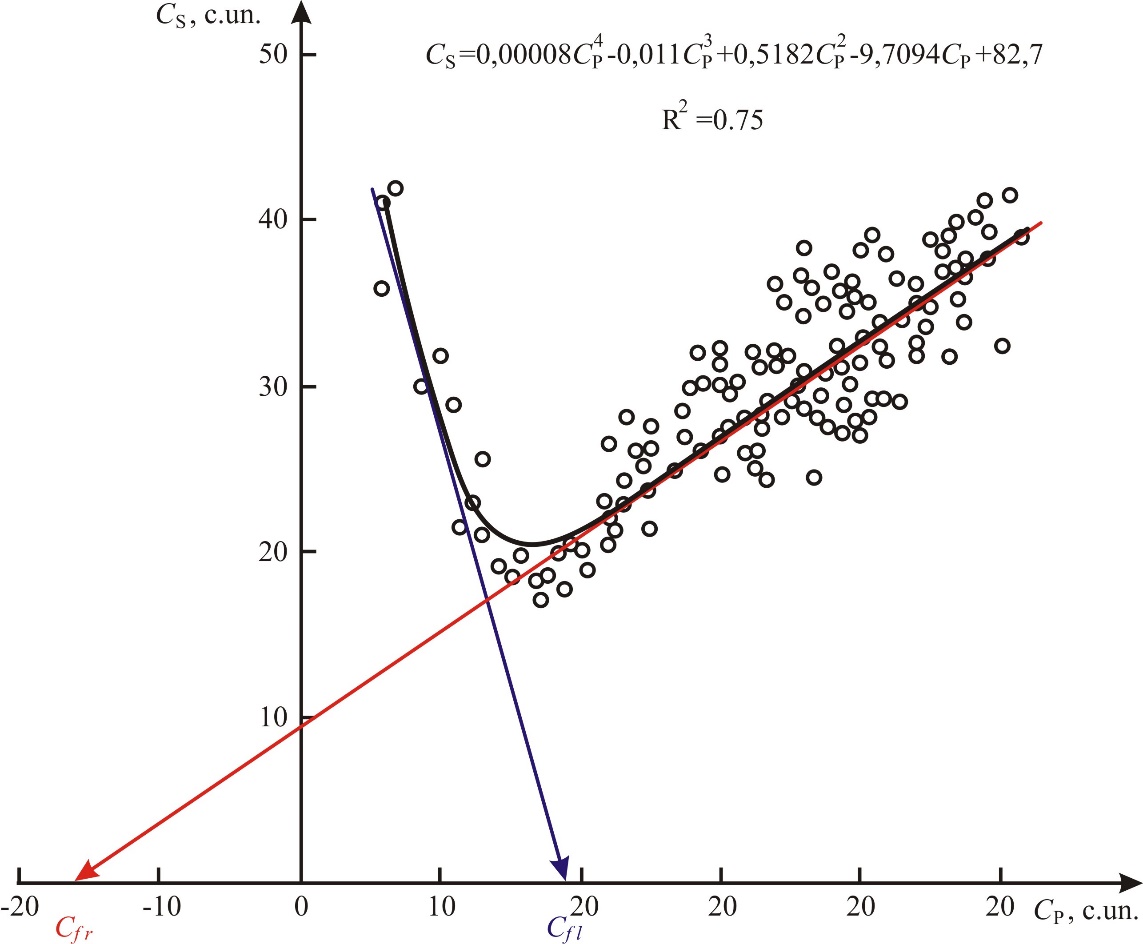
Figure 1 — The nature of change average oscillating velocity of transverse wave, depending on the average oscillatory velocity of longitudinal wave

As can be seen from the dependence (Figure 1), the oscillatory velocity of transverse wave decreases to some extent, and then begins to grow. According to core data, it is evident that with the value of K_p equal to 10% decreases by exponential law, and with porosity more than 10% it begins to grow. Average oscillating velocity of transverse wave () in the region of small porosities decreased towards its increased and starting with some value (8 … 10%) increased.

As can be seen from the dependence shown in Figure 1, the value for the right-hand side will acquire a negative value. On the other hand, according to (1), the value cannot be negative. Analyzing the process of interaction between longitudinal and transverse oscillations in a wave acoustic field, we obtained not the oscillatory velocity of longitudinal wave in the porous fluid, but the magnitude taking into account the influence of the porous fluid vibrations on the oscillatory velocity of longitudinal wave in reservoir rock, which is the basis for determining the porosity coefficient. That is, judging from the received, the authors [1,3,4] illegally in the equation (1) neglected the last member in the right sentence (K_r^ef·ρ_f·). Even if , according to our data, K_p^core=28 % and known , according to the calculation formula (3), we do not obtain a satisfactory result that would correspond to the average oscillatory velocity of longitudinal wave in the rock skeleton. If you look at formula (1), then the resulting value (let’s denote it ), which takes into account the influence of fluid fluctuations on the average oscillatory velocity of longitudinal wave, can be interpreted as follows.

For small porosity values 1.5-10%, the last member of the right part can indeed be neglected. With the increase in the open porosity that most use, the permeability rate increases sharply, and accordingly, the coefficient of effective porosity. Under these conditions, in the formula (1) the last member on the right side of the equation works (K_p^ef·ρ_f·). It leads to reduce the size of the right side faster than it can decrease due to the change ρ_r. With an increase open porosity, filtration increases and K_p^ef. As a result, with a certain value of porosity, the second and third terms of the right-hand side of equation (1) become equal and . With the subsequent change in porosity (in the direction of increase), the third term (K_p^ef·ρ_f·) prevails the second (K_p^ef·ρ_f·) and as a result.

Since the value is difficult to estimate and the coefficient of effective porosity is unknown, then for determination the porosity coefficient according to the data of the average oscillatory velocities of longitudinal wave, in the absence of the dependence «core-geophysics», based on statistical data, we derive the formula:

. (4)

By ρ_f we accept the density of the filtrate drilling mud as the main one, in the presence of a hydrodynamic imbalance between the drilling fluid and the fluid that affects the energy exchange between the stationary flow of the fluid and the acoustic field within the radius of the study by the method of acoustic oscillations.

It should also be noted that the critical values і  for different sediments and specific hydrodynamic conditions will be different. If there are in the cross-section reservoir with K_p<10 % we will have only the left branch, and with K_p>10 % — the right. When changing K_p≈2…13%, that is, in a wide range — two branches.

We propose a method for determining the magnitude that takes into account the influence of fluid fluctuations and its hydrodynamic state on the magnitude of average oscillatory velocity of longitudinal wave:

1. compare the values of average oscillating velocities of longitudinal and transverse elastic waves;
2. the points of intersection averaged lines for the right and the left axis with the axis will show the range of variation value for specific sediments and hydrodynamic conditions;
3. after this the choice of value is carried out as follows:

— for rocks, whose oscillation velocity varies from  cond.un. to  cond. un., the value is taken (the intersection with the axis tangent left branch);

— for rocks with an oscillatory velocity greater than, the value will be reduced from the value to the difference between and . For example, (Figure 2), , the intersection tangent left branch of dependence 2 indicates the value, in our case, >, therefore .

This method of determination will have the advantage over other methods that in our case the value should be regarded as a specific physical component of the wave acoustic field, which depends on many above factors and is determined for specific conditions.

For calculations in equation (4), we take the value of fluid density ρ_f from the priori information about the drilling fluid filtrate density. In our case, ρ_f = 1130 kg/m³. The value of the rock skeleton density can be found from the priori information about its mineralogical composition.

As a result of calculation, we give a graph of comparison the porosity coefficients calculated according to our method with the coefficients of porosity determined from the core material (Figure 2).

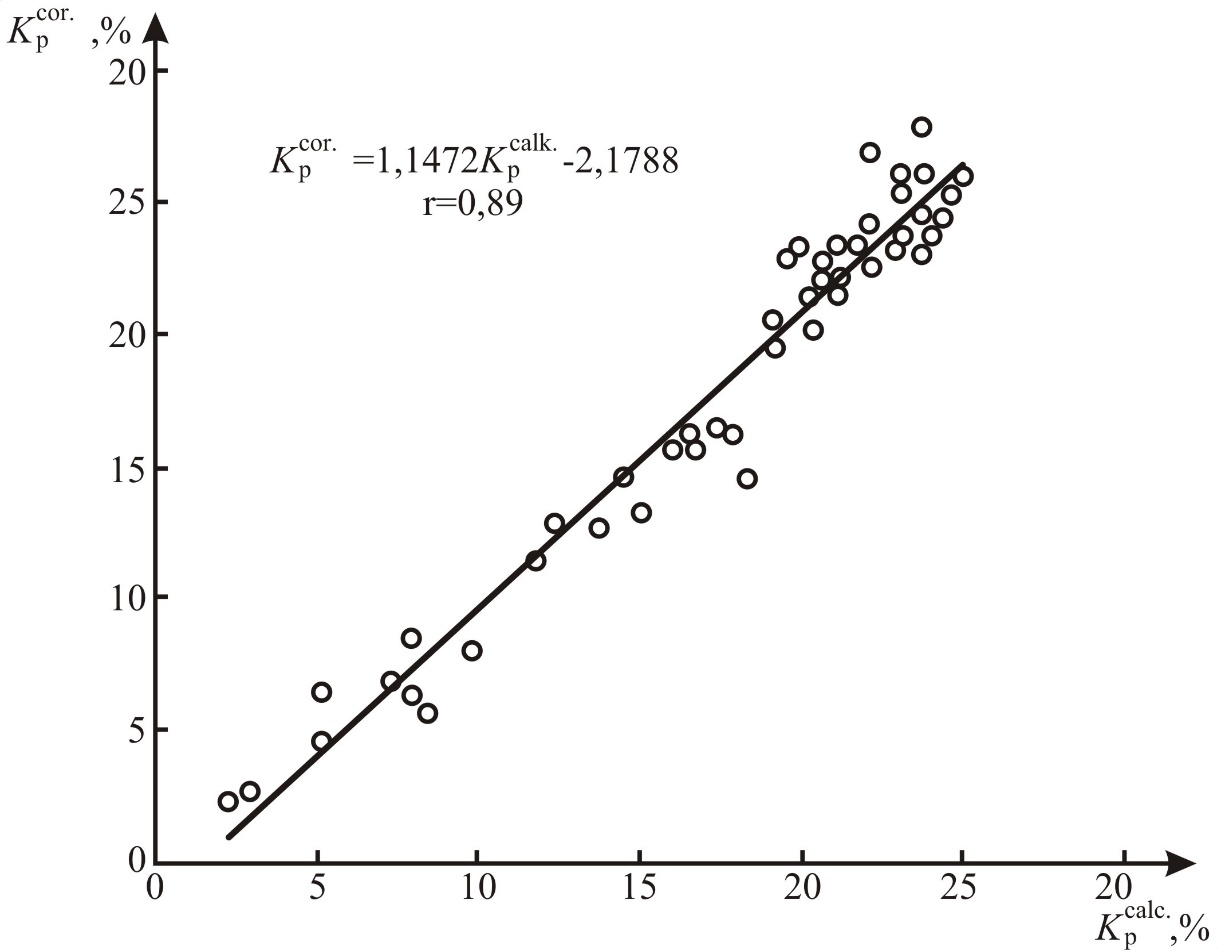
Figure 2 — Correlation of porosity coefficients determined by the core and average oscillatory velocity of longitudinal wave

Conclusions. Summarizing the above, we can conclude that the methodical approach to determining the coefficient of reservoir rock porosity with the help of data about magnitude oscillatory velocities is sufficiently effective and can be used for gas and gas-condensate fields such as the Dniprovo-Donetska depression and Precarpathian foredeep.

Literature

1. Kratkoe metodicheskoe rukovodstvo po interpretatsyi datyh dinamicheskogo karotaja. VNIIGeofiiki, 1986.
2. Ivakin B.N., Karus E.V., Kuznetsov O.L. Akusticheskyi metod isledovaniia skvajyn. — M.: Nedra, 1978. — 320 p.
3. Willie M.R.J., Gregory A.R., Gardner L.W. Elastic wave velocities in heterogeneous and porous media // Geophysics. – 1956. – V. 21, № 1. – P. 41 – 70.
4. Methods and apparaturs for acoustic logging through casing. [Schlumberger Technology Corp.]: Pat. kl. 340 – 15.5 ВН, (G01V1/40), № 3909775 USA/ Lavigne J.C.; Decl. 26.10.73, № 409.788; Publ. 30.09.75.
5. Raymer L.L., Hunt E.R., Gardner J.S. An improved sonic transit time — toporosity transform // SPWLA 21^st Annual Logging Symposium. 1980, July 8 — 11.
6. Kreif M., Garat J., Stellingwerf J., Ventre J. A petrophysical interpretation the velocities of P and S wave (full- wavtform sonic) // 12th International Formation Evaluation Symposium. – 1989, October 24.
7. Biot M.А. Theory of propagation of clastic waves in a fluid – saturated porovs solid. Part I – II. j. Acoust. SOS. Amer. – 1956. –28. –P. 168 – 175.
8. Halliburton Logging Services Chart Book / 1991, Halliburton publication.
9. Heysses D.R. Sonic poroste transforms and effects of pore shale and clay distribution // Halliburton Energy Services. Х1078. – 1995. – P. 1 — 13.