БАЛЛАДА О ЗОЛОТОМ КЛЮЧИКЕ К МАШИНЕ БЕЗ ВРЕМЕНИ

УДК 519.71

Светлой памяти моей незабвенной Светланы

БАЛЛАДА О ЗОЛОТОМ КЛЮЧИКЕ К МАШИНЕ БЕЗ ВРЕМЕНИ

BALLAD ABOUT GOLD KEY TO THE MACHINE WITHOUT TIME

В.А. Подчукаев

V.A. Podchukaev

Саратовский государственный технический университет имени Ю.А. Гагарина

Саратовский государственный аграрный университет имени Вавилова

Юго-Западный государственный университет, г. Курск

Институт проблем точной механики и управления РАН, г. Саратов

Саратовская государственная юридическая академия, 410028, Саратов, Россия

E-mail: sstu85@yandex.ru

Концепция Л. Эйлера раздельного рассмотрения трансляционного движения центра масс с линейными скоростями и спинорного вращения с угловыми скоростями дополнена концепцией слияния этих движений в совместное винтовое движение центра масс и центра смещения по траектории двойной спирали (аналогичной спирали ДНК). В основе дополнения лежит наполнение происхождения «центра смещения» физическим содержанием главных и осевых моментов инерции, что обусловлено кинематической конструкцией роторов векторных полей линейных и угловых скоростей. На основе введённых понятий зеркального отражения с искажениями и без искажений квантовые резонансы топологических переходов ветви равнобочной гиперболы из I квадранта в III и обратно интерпретированы как реверс первого рода (лента Мёбиуса) и второго рода (лист Мёбиуса). Показано, что двойная спираль траектории движения центра масс и центра смещения, обусловлена спиральными движениями на ортогональных поверхностях крестообразного полого объёмного резонатора, порождающего квантовые резонансы динамических систем. Эта двойная спираль является результатом поступательного и одновременно вращательного движения треугольника Пифагора вдоль строительной оси катета начальных угловых и линейных скоростей, образующих геликоид в пространстве возможных состояний. Замкнутая на себя траектория винтового движения двойной спирали интерпретирована как центрифуга из вписанного в неё тороида с центром в виде глоболоида (он же «бесконечный винт И.А. Вышнеградского»). На основе механизма деформации тора в гиперпараболоид 2-го рода 2 порядка разработан механизм перехода в аффинное пространство, описываемое однополостным гиперболоидом вращения (он же двухполостной гиперболоид вращения), квадратом гиперболы и удвоенным квадратом треугольника Пифагора, объединённых в одно геометрическое тождество для синтеза нелинейных пространственных траекторий движения.

The concept of L. Euler of separate consideration of the translational motion of the center of mass with linear velocities and the spinor rotation with angular velocities is supplemented by the concept of merging these motions into a joint helical motion of the center of mass and the center of displacement along a double helix trajectory (similar to the DNA helix). The basis of the addition is the filling of the origin of the «center of displacement» with the physical content of the axial moments of inertia, which is due to the kinematic design of the rotors of the vector fields of linear and angular velocities. On the basis of the introduced concepts of mirror reflection with distortions and without distortions, quantum resonances of topological transitions of a branch of an equilateral hyperbola from I quadrant to III are interpreted as a reverse of the first kind (Möbius strip) and the second kind (Möbius strip). It is shown that the double helix of the trajectory of the center of mass and the center of displacement is due to the spiral motions on the orthogonal surfaces of a cross-shaped hollow volume resonator, generating quantum resonances of dynamic systems. This double helix is the result of the translational and at the same time rotational motion of the Pythagorean triangle along the construction axis of the leg of the initial angular and linear velocities that form the helicoid in the space of possible states. The trajectory of the double helix movement closed in itself was interpreted as a centrifuge from a toroid inscribed into it with a center in the form of a globoloid (also known as the “endless screw of I. Vyshnegradsky.” into the affine space described by a one-cavity hyperboloid of revolution (also known as a two-cavity hyperboloid of revolution), a square of a hyperbola, and a double square of the Pythagorean triangle combined into one geometric identity for non-linear spatial shapes.

Ключевые слова: центр тяжести, центр смещения, двойная спираль, тороид, глоболоид, центрифуга, геликоид, треугольник Пифагора, лента и лист Мёбиуса, бесконечный винт И.А. Вышнеградского, гиперпараболоид, гиперболоид, рулетта, зеркальное отражение с искажением и без

Keywords: center of gravity, center of displacement, double helix, toroid, globoloid, centrifuge, helicoid, Pythagorean triangle, infinite screw I.А. Vyshnegradsky, Möbius strip and sheet, hyper paraboloid, hyperboloid, roulette, mirror image with and without distortion

Введение. Статья посвящена двойной спирали траекторий винтового движения центра масс и центра смещения динамических систем. Облечена в форму конспекта урока по геометрии в классической Юношеской Математической Школе (ЮМШ). Курсивом выделены фразы учителя геометрии. Остальной текст предполагается разместить на слайдах, сопроводив их фрагментами музыкального сопровождения сообразно содержанию. Музыкальные фрагменты выделены курсивом с подчеркиванием, предшествующим очередному смысловому содержанию. Эти фрагменты желательно использовать в качестве медийного сопровождения урока (интернет-ссылки указаны).

1. Конспект урока.

В.С. Высоцкий. Баллада о борьбе [https://.youtwwwube.com/watch?v=zLuXmoZnrTw].

Анализ уровня соответствия аудитории окружающей физической реальности: Уважаемые коллеги! Кто из Вас слушал детскую синтез-оперу Льва Конова «Асгард»? Так вот: «Тор – это не персонаж из грошовой оперы, и не персонаж из анимэ Забавы Богов, и уж тем более не название твердотельного накопителя (SSD), выпускаемого под брендом е2е4, и даже не 90-й элемент в таблице Д.И. Менделеева (вы даже знаете, что это торий). Но тор это , вообще говоря, совсем не то, что Вы думаете. Да, и не астероид (299) Тора, и уж тем более не иудейская Тора. Тор – это сказка, да не про белого бычка, тор — это надувной спасательный круг человечества (он же бублик) из нелинейного пространства аффинной геометрии 4-х измерений, он же тема нашего урока. Урок посвящён интуиционистской математике Германа Вейля. Кто это? Посмотрите в органайзере для домашних заданий WIKI2.org.

Тор (от лат. Spira – спираль) связан с именами двух геометров Эллады: Архита Тарентского (задача об удвоении куба – отыскание точки пересечения трёх поверхностей: конуса, цилиндра и тора) и Персея (первооткрыватель спиралей, названных им спирическими линиями, позднее переименованными в кривые Персея). Открытый тор представляет собой плоскую алгебраическую кривую четвёртого порядка [1, С. 73, таблица 5] в пространстве 4-х измерений

(1)

где – расстояние от центра образующей окружности до оси вращения, – радиус образующей окружности

 (2)

В соответствии с аффинной классификацией нелинейных поверхностей саратовской школы геометров и алгебраистов всемирно известного профессора В.В. Вагнера [2] тор (1) в [1] классифицирован как гиперпараболоид второго порядка 2-го рода в новой координатной системе, отличной от исходной и связанной с нею обозначениями

 (3)

позволившими записать (1) в виде так классифицированного гиперпараболоида

(4)

Процедура отображения (1) на (4) с искажением (3) основана на подстановке левой части (2) вместо r² в первое выражение в круглых скобках в (1)

(5)

откуда после введения новой координатной системы (3) имеем

.

Замена второго слагаемого левой части последнего равенства согласно (3) даёт

что позволяет полученное выражение переписать в виде

откуда следует (4).

Как видно из формул (3), (4) их крайние справа члены представляют собой сумму катетов 4 порядка треугольника Пифагора (или второе по счёту удвоение квадрата, первое удвоение сделал Пифагор). Иначе сумму биквадратов можно назвать «ключом» связи декартовых систем координат (x, y, z) со второй системой (3), описанной выше.

Отличное от (4) представление тора с использованием декартовой системы координат (3) сконструируем, заменив первые два слагаемых левой части (1) правой частью (2) из (1). В результате получим квадрат суммы квадратов в левой части следующего равенства

(6)

или, что — то же самое

 (7)

иначе квадрат разности квадратов

 (8)

который введением обозначения (будем называть его» «золотым ключиком Буратино»)

(*)

и переносом второго слагаемого левой части (8) вправо

можно переписать в виде

 (9)

Это (9) второе по счёту представление тора (1), первым является (4), можно назвать отражением (1) с одним искажением, носителем которого является «ключик» (* — он же зеркало в королевстве кривых зеркал, куда любит путешествовать Ваша любимая Алиса в машине без времени. Её, да не Алису, мы опишем ниже).

Левая часть (9) и правая часть (4) совпадают, что позволяет получить ранее не описанное «тождество троичной логики» в обозначениях Бернхарда Римана (здесь и далее будем называть его машиной без времени)

в котором перенос крайнего справа слагаемого в середину даёт

Нетрудно видеть, что поворот «ключика» с искажением (ключ тот же самый, левая часть последнего тождества становится невидимой, видимы средняя и правая часть «тождества троичной логики»), то есть видна формула сокращённого умножения или возведения в квадрат (он же показатель степени «2») разности квадратов (правая часть), тем самым срединная и правая часть последнего из полученных тождеств суть одно и то же.

Следовательно, «ключик» можно вынуть из середины, получив классическое (не троичное) тождество, иначе открыв «дверь» (за нарисованным очагом в комнате папы Карло) назад из пространства 4-х измерений в пространство 3-х измерений. Делением обеих частей получившего тождества на 4R² (R≠0) получим из правой части гиперболу, возведённую в квадрат

Открыв тем самым следующую «дверь» в пространство 2-х измерений, которое последующим делением на приведенную выше гиперболу даёт однополостный гиперболоид вращения

изображённый на рисунке

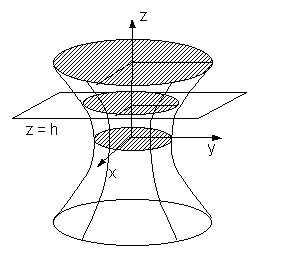
Рис. 1. Однополостный гиперболоид вращения

Умножение обеих частей уравнения однополостного гиперболоида вращения на «(-1)» даёт двуполостный гиперболоид вращения. Он является результатом вращения зеркального отражения без искажения (реверс II рода) квадрата гиперболы вокруг биссектрисы II и IV квадрантов (неважно по часовой или против часовой стрелки). Это возвращение из пространства двух измерений в пространство 3-х измерений.

Про реверсы и зеркальные отражения, я расскажу после, не перебивайте. Описанное путешествие по пространствам ассоциируется с машиной без времени (не путайте с различными вздорными инсинуациями о машине времени). Наша машина без времени – это фазовое пространство, в котором времени нет (на уроках нерелятивистской физики Вам о нём говорили. Время придумано человечеством, а оно (человечество) может ошибаться, потому что у него есть коллективная душа, называется ноосферой В.И. Вернадского, на уроках физики Вам расскажут о его «матрёшке». Ещё с ней поиграете. Долго будете играть. Скорее всего до седых волос.

Для того, чтобы наделить тор качествами движущегося объекта посредством линейных и угловых скоростей, включая моменты инерции, в качестве субъекта движения возьмём осесимметричный летательный аппарат (ОЛА), винтовое движение которого описывается роторами линейных и угловых скоростей

которые после перемножения с использованием операции скалярного умножения матриц «⊗» [3, C. 42] дают

Кинетическую энергия спинорного вращения ОЛА вокруг всех строительных осей ССК по аналогии с кинетической энергией, порождаемой движением линейными скоростями, принято вычислять по формуле

но эта формула – неправильная, потому что движение с линейными скоростями, как правило, осуществляется в одну сторону, а с угловыми скоростями как по часовой стрелке, так и против. Поэтому правильной формулой будет возведение в квадрат предыдущей формулы.

Осевые моменты инерции АТТ вычисляются по хорошо известной формуле

где mi  — масса точки, pi — расстояние от i-ой точки до соответствующей оси. Вдоль осей x и y применительно к ОЛА соответствующие им осевые моменты инерции равны и постоянны чего нельзя сказать об осевом моменте инерции Iz , что видно из формулы следующей «экспоненциальной гиперболы» с переменным знаменателем для выгорающей массы, полученной в [4, C.18, формула (17)]

(10)

Искривление траектории винтового движения вдоль вертикальной оси ввинчивания треугольника Пифагора в окружающее пространство находит простое объяснение другой формулой [4, C.18, верхняя формула в (18)], в которой участвует уже «классическая» гипербола

 (11)

Сравнением (10) с (11) получим следующее тождество для касательной к траектории трансляционного движения изображающей точки z

 (12)

которое является ничем иным, как определением производной или скоростью трансляционного движения вдоль траектории движения z.

Этот тривиальный, на первый взгляд результат, имеет далеко идущие последствия в силу того, что и производная, и интеграл от показательной функции равны самой показательной функции, делая математические операции дифференцирования и интегрирования ничтожными.

В.В.С. Высоцкий. «Дорогая Передача». [ https://www.youtube.com/watch?v=-CFqhVQj-qA]

Замечание. Тем самым, такой раздел математики как математический анализ с его дифференциальным и интегральным исчислениями приказал долго жить, как одно из заблуждений человечества. Другими словами, математические операции дифференцирования и интегрирования должны быть исключены из рассмотрения, иначе подвергнуты реверсу II рода или делению на самих себя, изображаемому посредством четвертных и/или трёх четвертных нот. В итоге получится ЕДИНИЦА (важная, выстраданная, давшая колоссальный скачок в познании), но при этом остающаяся 1-ей (Бога Одина), за которую человечество может получить оценку «отлично». Утешает, что начинать придётся не с чистого листа, а с листа Мёбиуса, то есть с возврата к истокам эллиннских знаний (Аристотель, Платон, Пифагор, Аполлоний Пергский, Архимед, Архит Тарентский…Михаэль Штифель (экспонента, иначе логарифм; биномиальные коффициенты; операция возведения в степень; операция извлечения корня), Ф.Виет, Р.Декарт, Л. Эйлер (обозначение и использование в качестве основания натурального логарифма трансцендентного числа е, впервые вычисленного Бернулли в задаче о ссудном проценте – проклятии человечества)…И.А Вышнеградский (диаграмма, возрождение гиперболы),Карл Вейерштрасс (нигде не дифференцируемая непрерывная функция, А.М. Ляпунов (показатель – скорость разбегания разнонаправленных движений, встречающихся в одной точке), Оскар Перрон (дихотомия – начало пути к золотому сечению)…, а это уже лента Мёбиуса.

Дополнительными факторами, влияющими на искривление траектории винтового движения, являются непредсказуемые воздействия окружающей среды в виде скоростного напора, что видно из формулы для кинетической энергии набегающего потока (ρ — плотность потока, разная для каждой сферы в «матрёшке» пары «биосфера-ноосфера В.И. Вернадского» [5])

Для простоты рассмотрим спиральный рукав траектории ОЛА до отстрела первой ступени. В нём криволинейная траектория набора высоты описывается экспонентой (12), которая в [6, C.456] ассоциирована с гиперболой при движении по последней снизу-вверх. Для вертикально расположенного тора (он же колесо с надетой на него камерой)

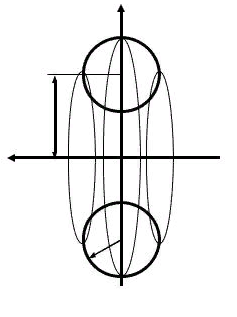
Рис. 2. Крутящееся колесо

Приведенный рисунок является геометрической моделью спиральной Галактики четырёх измерений по осям вращений (оси абсцисс и ординат вращений колеса, оси абсцисс и ординат плоских вращений малых кругов внутри камеры колеса), трёх измерений по осям линейных скоростей ССК, репера трёхгранника Френе главных и осевых моментов инерции, зависящих от распределения массы АТТ и геометрии конструкции ОЛА, включая изменяемую геометрию крыла (для самолёта или БПЛА) или отстрел ступеней для ОЛА.

Если колесо катить вперёд , то траектория движения будет описываться циклоидой, которую Паскаль называл более глубоким в смысле «руления по траектории» словом «рулетта».

Интерпретация изложенных выше результатов требует привлечения опыта практической рулёжки самолётом в тропосфере и стратосфере [7] на основе формализма «вращение-угол» [8]. При этом превращение плоских кривых в пространственные (на языке атрибутов движений и тензоров моментов инерции), может быть выполнено на основе плоских геометрических представлений, исчерпывающе изложенных в [9].

Тезаурус ключевых слов настоящей статьи следовало бы включить в новый словарь школьной информатики с целью подготовки нового поколения конструкторов-дизайнеров нелинейных пространств аффинной геометрии для конструрования машин и механизмов техносферы, создания систем искусственного интеллекта и нового поколения интегральных микросхем [10], но, в первую очередь, выстраданного выхода за пределы нашей колыбели без голливудских мистификаций.

Что такое зеркальные отражения и реверсы разных родов я расскажу дальше без использования понятия времени.

Фундамент аффинной геометрии нелинейных пространств скалярных и биторсионных полей динамических систем [4, 5] составляет понятие пространства возможных состояний (или возможных решений этих систем) [11], описываемое двумя сферами:

1) сферой линейных скоростей с фиксированным центром, ассоциируемым с центром масс (он же центр тяжести) или началом отсчёта в связанной системе координат (ССК) [4]

Скрытый сомножитель этого тождества в виде половины массы или половины плотности набегающего потока окружающей среды дают либо кинетическую энергию, либо скоростной напор;

2) сферой угловых скоростей со смещающимся центром относительно начала отсчёта [1, безымянный вектор D] в [12], получивший название вектора центра смещения и обозначение G

Там же, в [12], тождество с билинейным произведением векторов записано в виде центральной сферы переменного радиуса, ассоциированной в [3] с треугольником Пифагора (слева – квадрат гипотенузы, справа – сумма квадратов катетов)

иначе генератором пульсаций сферических волн [5, С. 456, утверждение].

Помимо сферических волн в пространстве возможных состояний, образованном ортогональными векторами начальных угловых скоростей и угловых скоростей центра смещения, имеют место спиральные волны, порождённые одновременным биторсионным кручением центра масс и центра смещения вокруг ортогональных осей [5]. Они описываются формулой равнобочной гиперболы (от др.-греч. ὑπερβολή, от ὑπερ— «верх» + βαλειν— «бросать»), она же динамический аналог [13] известной с древнейших времён (и потому не персонифицированной) формулы гармонического деления золотого сечения

в которой числитель описывает разнонаправленные трансляционные движения (в круглых скобках: влево-вправо) и в то же время встречно направленные спинорные вращения (по часовой стрелке (+) и против часовой стрелки (-) внутри скобок). Эти движения знаменатель дополняет обратно пропорциональным удвоенным вращением.

Иоганн Кеплер считал треугольник Пифагора и золотое сечение великим наследием Эллады, забыв упомянуть описанную выше гиперболу Аполлония Пергского.

Числитель формулы гиперболы для центра смещения (ось ординат) можно ассоциировать с «бросанием вверх», а удвоенный знаменатель для той же оси — с падением «вниз», которое не может не быть винтовой траекторией, состоящей из двух биторсионных вращений. При смене знака знаменателем имеет место квантовый скачок «вниз» (или свободное падение с вращением) ветви гиперболы из I квадранта в III:

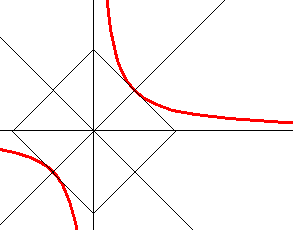
Рис. 3. Равнобочная гипербола

Топологический переход ветви гиперболы между этими квадрантами сопровождается увеличением вдвое длины траектории падения (с вращением), что в [8] названо квантовым резонансом, а в [14] идентифицировано как реверс I рода.

Ассоциируем изображающую плоскость (рис. 1) с лентой Мёбиуса. Ассоциация основана на склейке верхней полуплоскости рисунка с нижней, но полученной в результате двух «зеркальных» полуоборотов верхней полуплоскости сначала вокруг оси ординат, а затем (для того зеркального отображения, что получится при первом полуобороте) вокруг оси абсцисс. Итоговым результатом каждого полуоборота будут разные зеркальные отражения исходной верхней полуплоскости. Они, как и всякие зеркальные отображения, «хиральны» по отношению к оригиналу (то есть различны как левое и правое, верхнее и нижнее). Иными словами, рис. 1 – это лента Мёбиуса склейки верхней полуплоскости гиперболы со своим зеркальным отражением, полученным в результате двух хиральных искажений. Для простоты назовём его «зеркальным отражением с искажением». С ним отождествлён квантовый резонанс, или, как показано в [14], реверс I рода.

Но тот же самый квантовый резонанс имеет оборотную сторону медали в виде реверса II рода [14], который с помощью понятия «зеркального отражения без искажений» означает зеркальное отображение ветви гиперболы I квадранта на III квадрант, полученное полуоборотом плоского зеркала относительно диагонали (она же биссектриса) II и IV квадрантов. И это — уже не лента, а лист Мёбиуса.

В [14] реверсы обоих родов иллюстрируют две партитуры [14, рис. 2, 3] из двух последовательностей четвертных и трёхчетвертных нот, штиль которых ассоциирован с направлением спирального вращения траектории движения на фазовой плоскости: «вверх» (по часовой стрелке) – «вниз» (против часовой стрелки). Поскольку спираль траектории движения может рассматриваться либо как встречно направленное движение компонент вектора состояний навстречу друг другу (притяжение), либо как разно направленное (отталкивание), то «притяжение» иллюстрируется четвертными нотами, а «отталкивание» — трёх четверными.

Идея музыкального представления переходных процессов динамических систем аналогична идее метода главных компонент Пирсона [https://wiki2.org/ru/Метод_главных_компонентhttps] уменьшения размерности данных с наименьшей потерей информации, иллюстрацию которой демонстрирует следующий рисунок

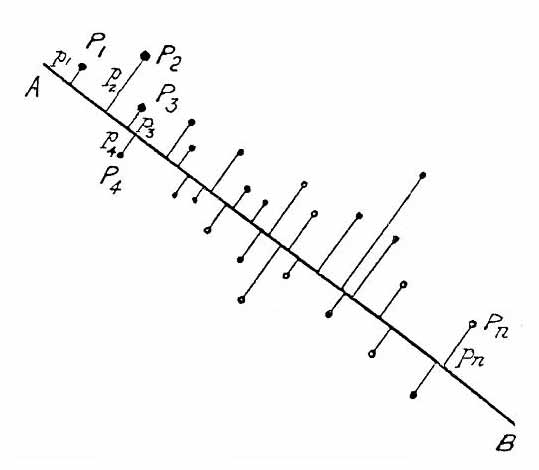
Рис. 4. Идея машинного обучения и data mining Карла Пирсона

Идею Пирсона дополняет реверс второго рода, обозначенный как деление ноты на саму себя, когда унаследованное направление штиля из предыдущего квадранта меняется на противоположное в квадранте с реверсом II рода (с последующим наследованием этого признака продолжением спирали, обратным по отношению к направлению штиля до точки реверса этого рода). Главным при этом является направление топологического перехода, а именно: по диагонали (то есть по прямой, а не по спирали, как до, так и после точки реверса этого рода) [14, строка 21 таблицы].

Описанные зеркальные отражения с искажением и без с использованием музыкальной нотации можно применять в алгоритмах криптографии для выбора нотного ключа, недоступного методам математической дешифровки, и в искусственном интеллекте автоматического анализа больших данных в качестве дополнительного метода их индексации.

Как показано в [5], поверхность, образуемая вращением гиперболы вокруг оси ординат центра смещения, даёт полый объёмный резонатор

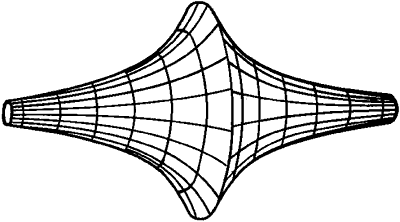
Рис. 5. Объёмный резонатор вращения гиперболы вокруг оси ординат

а вращение гиперболы вокруг оси абсцисс (вращение центра тяжести) даёт второй полый объёмный резонатор

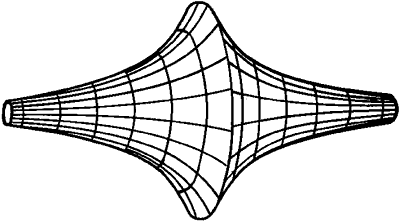
Рис. 6. Объёмный резонатор вращения гиперболы вокруг оси абсцисс

Вдавленные один в другой эти объёмные резонаторы образуют общий крестообразный полый объёмный резонатор [5, 6]. Отметим, что каждую из псевдосфер этого резонатора можно отождествить с по-разному ориентированными солитонами.

Проекция траектории движения изображающей точки по гиперболе на плоскость экваториальной окружности каждого из резонаторов рисунков 5 и 6 даёт две ортогональные в трёхмерном пространстве плоские спирали Архимеда, закручивающиеся в разных направлениях либо по направлению к центру, либо от центра в зависимости от положения наблюдателя (для рис. 5 сверху или снизу, для рис. 6 – слева или справа). В центре крестообразного резонатора эти спирали перекрещиваются не пересекаясь, что позволяет считать этот резонатор биторсионым генератором спиральных волн.

Тем самым концепцию Л. Эйлера раздельного рассмотрения трансляционных движений с линейными скоростями и спинорных вращений с угловыми скоростями необходимо дополняет концепция винтового движения, описываемая кинематической конструкцией ротора У.Клиффорда для билинейного члена для уравнения сферы угловых скоростей со смещённым центром, который с помощью операции «скалярного умножения матриц» [3, C. 42, обозначение «⊗»], распространяющейся и на векторы, имеет следующее представление

где через I обозначен вектор главных осей инерции «момента количества вращения» [13], зависящий от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Этот вектор через осевые моменты инерции строительных осей ССК представляется в виде

объясняя тем самым физическое происхождение центра смещения.

Динамическое поведение совместного спирального разнонаправленного и/или встречно направленного движения изображающих точек центра тяжести и центра смещения в трёхмерном пространстве описывает двойная спираль, принадлежащая поверхностям описанного выше крестообразного полого объёмного резонатора, а геометрическим образом их совместного движения одна относительно другой является гипотенуза треугольника Пифагора сложения угловых скоростей, на которой центры масс и смещения могут меняться местами, то есть иметь как разно направленные, так и встречно направленные траектории движения.

Добавляя к геометрической интерпретации билинейного члена ротор векторного поля линейных скоростей

умножением «⊗» слева на крайнее справа выражение в приведённых выше формулах окончательно получим образ совместного трансляционного движения с линейными скоростями и спинорного вращения с угловыми скоростями с учётом момента количества вращения, иначе винтовое движение

В качестве физических явлений, которые могут получить объяснение на основе понятия «центр смещения» можно привести:

1) флаттер (в тропосфере), сопровождавший разрушение самолёта, при преодолении им звукового барьера на заре развития реактивной авиации до тех пор, пока не стали принимать во внимание так называемый аэродинамический центр (он же центр смещения, обусловленный скоростным напором набегающего потока окружающей среды и моментами инерции абсолютно твёрдого тела), смещённый относительно центра тяжести и закладываемый на этапе конструирования исходя из результатов обдува в аэродинамической трубе. Следующая фотография преодоления звукового барьера иллюстрирует верхнюю псевдосферу Н.И. Лобачевского объёмного резонатора, изображённого на рис. 5, который унёс не одну сотню жизней лётчиков-испытателей разных стран вследствие квантового резонанса, приводившего к разрушению самолёта:

Рис. 7. Преодоление звукового барьера

2) «гайку Джанибекова» (в невесомости), периодически меняющую направление вращения на противоположное вследствие квантового резонанса угловой скорости центра смещения вдоль её оси вращения. Естественно ожидать, что для громоздких космических конструкций учёт динамического поведения центра смещения относительно центра масс является первостепенной задачей обеспечения безопасности полётов обитаемого космического аппарата;

3) «якобы просверленное отверстие» в оболочке МКС вполне может найти объяснение как термодинамический квантовый резонанс, являющийся результатом воздействия скоростного напора набегающего потока ионизированного атомарного кислорода (в термосфере Земли) на поверхность герметизированных отсеков станции (с унаследованными линейными скоростями трансляционного движения Земли).

На рис. 9, 9 фотографий декабрьского старта ракеты-носителя с космодрома «Восточный» двойная спираль (аналогичная двойной спирали ДНК) траектории совместного винтового движения центра тяжести и центра смещения видна невооружённым глазом как инверсионный след ракеты-носителя до отстрела первой ступени:

1) первые секунды после старта

Рис. 8. Инверсионный след первых секунд после старта

Двойную спираль нельзя не увидеть в нижней части фотографии инверсионного следа. То обстоятельство, что двойная спираль обусловлена разнонаправленными движениями подтверждается числителем формулы для гиперболы и не может не вызвать ассоциации с известным с древности кадуцеем (от лат. Caduceus – жезл Гермеса и/или глашатаев), что продемонстрировано в [15, P.145, Fig. 4] применительно к центрам смещения ауры биополей вдоль позвоночника,

2) инверсионный след полёта ракеты-носителя до отстрела первой ступени представляет собой искривлённую траекторию движения, напоминающую искривлённый рукав выхода на круговую орбиту (или замкнутую траекторию)

Рис. 9. Инверсионный след рукава двойной спирали, предшествующий выходу на замкнутую траекторию движения

Сконструировать возникновение двойной спирали можно поворотом плоскости треугольника Пифагора вокруг катета начальных угловых скоростей, направленного вертикально вверх по строительной оси связанной системы координат (ССК). Выбор этого катета не случаен и основан на доказанной в [4, C. 10] «теореме о неподвижной точке» обеих сфер (линейных и угловых скоростей), потребовавшей обобщения понятия ротора линейных скоростей на размерности пространства состояний, большие трёх (у У. Клиффорда размерность ротора – три). В обоснование такого обобщения ниже приведена аффинная классификация тороида как геометрического объекта в пространстве 4-х измерений.

Сообщим катету начальных угловых скоростей и, как следствие, всей ССК угловых скоростей, направление трансляционного движения вдоль этого катета с начальными линейной и угловой скоростями. Тогда результатом поступательного движения треугольника Пифагора вдоль строительной оси ССК и его вращения вокруг этой оси будет прямой конус с образующей в виде гипотенузы треугольника. На ней будут находиться (разнесённые в трёхмерном пространстве, но принадлежащие гипотенузе) изображающие точки центров тяжести (принадлежит спирали на поверхности рис. 6) и смещения (принадлежит спирали на поверхности рис. 5). Через любую точку образующей поступательно движущегося и одновременно вращающегося конуса (то есть гипотенузу) можно провести секущую плоскость, параллельную плоскости образующих конуса, которой принадлежит катет начальных угловых скоростей. Пересечение секущей плоскости с поверхностью конуса даёт блуждающую гиперболу разнонаправленных движений числителя гиперболы. Эта гипербола будет принадлежать винтовой поверхности геликоида, образованного перпендикулярным к оси вращения и одновременно поступательным движением катета центра смещения. Винтовая поверхность геликоида (аналог – «Архимедов Винт») изображена на следующем рисунке

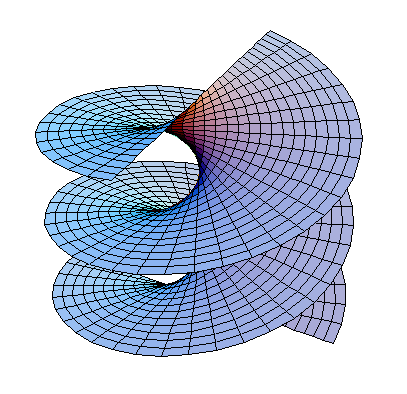
Рис. 10. Геликоид

Таким образом любой незамкнутый отрезок траектории движения геликода будет представлять собой спиральный рукав двойной спирали (рис. 8, 9) движения центра тяжести и центра смещения, а в случае её замыкания — тороид, допускающий дуальное физическое толкование: как вписанный в двойную спираль или описанный вокруг неё

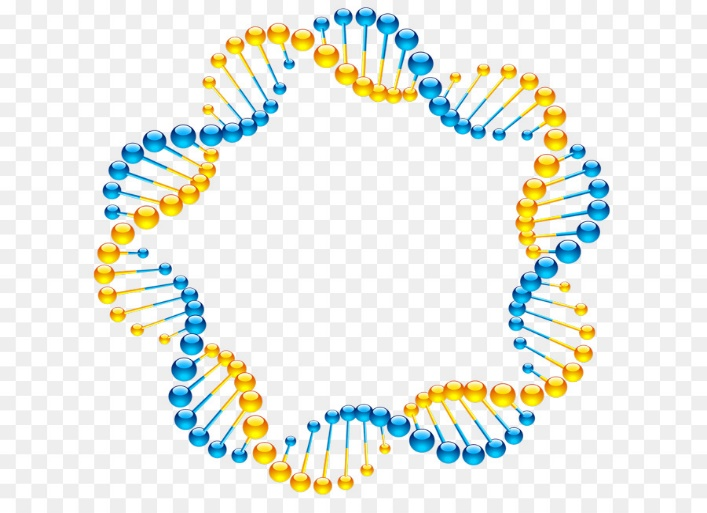
Рис. 11. Тороид

Для вписанного тороида описание четырёхмерным пространством представляется излишним, поскольку исходя из физических соображений его можно ассоциировать с центрифугой [13, C. 1116], образованной кольцом, натянутым на глоболоид

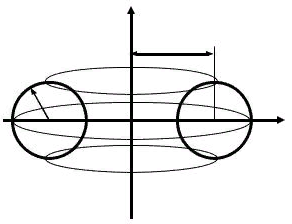
Рис. 12. Центрифуга

В центре центрифуги — глоболоид, иначе внутренность обода вращающегося колеса. Сам глоболоид можно ассоциировать с вогнутым «бесконечным винтом И.А. Вышнеградского» [16, C. 442], изображённым на следующем рисунке

Рис.13.Глоболоид.

Глоболоид вращается либо по часовой стрелке, либо против. Центрифуга описывает механизм передачи вращения со смещением на тороид, иначе гипоидную (гиперболоидную) передачу [https://wiki2.org/ru/Гипоидная_передача], известную в теории механизмов и машин. Реверс глоболоида будет означать изменение направления навивки двойной спирали его резьбы.

Резюмируя изложенное, можно заключить, что основными результатами статьи являются:

1) концептуальное наполнение понятия «центр смещения» физическим содержанием осевых моментов инерции, что обусловлено кинематической конструкцией обобщённого ротора векторного поля линейных скоростей, записываемого посредством угловых скоростей [4, C. 10] как

в соответствии с четырьмя характеристиками траекторий движения: «вверх-вниз», «вперёд-назад», «влево-вправо», «по часовой стрелке-против часовой стрелки»). Этот обобщённый ротор позволяет ассоциировать квантовый резонанс с реверсами I рода (как зеркальное отражение с искажением или ленту Мёбиуса) и II рода (как зеркальное отражение без искажений или лист Мёбиуса),

2) концептуальное дополнение концепции Л. Эйлера движения центра масс с линейными скоростями и вращения вокруг центра масс с угловыми скоростями винтовым движением (симбиоз одновременно трансляционного движения и спинорного вращения) в форме двойной спирали (аналогичной двойной спирали ДНК) траекторий движения центра тяжести и центра смещения, обусловленных главными и осевыми моментами инерции абсолютно твёрдого тела,

3) на основе механизма деформации тора в гиперпараболоид 2-го рода 2 порядка разработан механизм перехода в аффинное пространство четырёх измерений, описываемое гиперболоидом 3-го порядка, квадратом гиперболы и биквадратом треугольника Пифагора, объединённых в одно геометрическое тождество для синтеза нелинейных пространственных траекторий движения.

Общий вывод: движение в окружающем пространстве физической реальности описывается криволинейными трансляционными, спинорными и винтовыми траекториями нелинейных пространств аффинной геометрии. Бесконечность (или деление на ноль, к которому настороженно относятся со времён Эллады) наполняется физическим содержанием (конечного по сути), но в то же время «бесконечного винта И.А. Вышнеградского» и бесконечной ленты Мёбиуса. При этом феномен возникновения центра смещения объясняется заложенными при конструировании главными и осевыми моментами инерции. Они обуславливают искривление траекторных движений относительно унаследованных при старте (в качестве начальных) угловых и линейных скоростей Земли. Траекторные движения принадлежат нелинейным пространствам аффинной геометрии, сконструированным без привлечения понятия гравитации поскольку то, что понимают под нею, исчерпывается понятием центра смещения и характеристикой движения как «встречно направленного (притяжение)» или «разнонаправленного (отталкивание)» (она же пятая характеристика траекторий движения в дополнение к четырём перечисленным выше).

2. Окончание урока.

В.И. Агапов. «Прощание славянки».Всенародно любимый «перронный марш».

[https://www.youtube.com/watch?v=gO2q0Tru5S8]

Домашнее задание. Желательно подготовить к следующей неделе. Нужно модифицировать формализм кортежа и маски теории систем искусственного интелекта, изложенный в последних главах [10], заменив имеющийся там набор математических операций для работы с большими данными на музыкальную нотацию. Подсказки: 1) выкинуть операции дифференцирования и интегрирования, заменив их операциями логарифмирования и антилогарифмирования; 2) обе ленты Мёбиуса наделить качеством нотного стана из пяти линеек, чтобы с его использованием можно было снабдить каждую ноту атрибутом частоты издаваемых ею колебаний; 3) подготовить нотное послание для Вселенной с кратким музыкальным фрагментом из «Прощания Славянки» Агапова. Что будет означать: «Ух ты, мы вышли из бухты» (не путать с гаванью, которую любят некоторые президенты).

Переходим к обсуждению. Мне интересны Ваши мнения, касающиеся измышлений всемирно известного сказочника Хокинга по поводу устройства Вселенной в свете того, что Вы увидели и услышали на нашем уроке. И не является ли его фигура неким собирательным медийным персонажем типа группы «не Бурбаки», присутствующим в ноосфере ссудного процента Якоба Бернулли? (она же группа оглупления).

В.С. Высоцкий. Баллада о «Правде и лжи»

[https://www.youtube.com/watch?v=dgSKHtwiaVo]

СПИСОК ЛИТЕРАТУРЫ

1. Подчукаев В.А. «Великие» проблемы физики и «физического минимума» (в смысле В.Л. Гинзбурга) глазами инженера от «искусства управления» // Доклады Академии военных наук. 2013. № 5 (59). Вып. 1. С. 5-75. http://www.twirpx.com/file/1937329/
2. Пензов Ю.Е. Аналитическая геометрия. Саратов: изд-во Сарат. Ун-та, 1972. 364 с.
3. Подчукаев В.А. Теория автоматического управления: аналитические методы. М.: Наука, 2005. 392 с. ISBN 5-9221-0445-4.

https://www.twirpx.com/file/1957755/

1. Подчукаев В.А. Анализ скалярных полей динамических систем//Известия ВУЗов. Приборостроение. 2016. Т. 59, № 1. С. 5-24. DOI: 10.17586/0021-3454-2016-59-1-5-24. http://pribor.ifmo.ru/ru/article/14630/analiz_skalyarnyh_poley_dinamicheskih_sistem.htm/14360.pdf
2. Подчукаев В.А. Объёмные резонаторы скалярных полей динамических систем//Известия ВУЗов. Приборостроение. 2018. Т. 61, № 6. С. 477-484. DOI 10. 17586/0021-3454-2018-61-6-477-484. http://pribor.ifmo.ru/file/article/17862
3. Подчукаев В.А. Квантово-волновой дуализм описания динамических систем // Мехатроника, автоматизация, управление. 2016. Т. 17. № 7. С. 453-457.

DOI 10.17587/mau. 17453-457.

https://mech.novtex.ru/jour/article/view/326/187https://mech.novtex.ru/jour/article/view/326/187.

1. Крылов А.М., Степанов П.П. Бытко С.А., Подбереженский В.С., Алещенко В.П. Практическая аэродинамика и боевое маневрирование самолётов. Монино, Военно-Воздушная Академия, 1984. 520 с.
2. Подчукаев В.А. Формализм «вращение-угол» в теории скалярных полей динамических систем//Мехатроника, автоматика и робототехника. 2017. № 1. С. 70-72. http://elibrary.ru/downljad/elibrary 28859157 65451791.pdf
3. Савёлов А.А. Плоские кривые. Систематика, свойства, применение (справочное руководство)/Под ред. А.П. Нордена. М.: Физматлит, 1960. 293 с.

https://www.twirpx.com/file/2130315/

1. Подчукаев В.А.  Автоматическое проектирование информационно-управляющих систем. Автоматический синтез топологии вычислительного ядра встраиваемых систем, LAP LAMBERT Academic Publishing Gmbh & Co KG, Saarbruken (Germany), 2012 , 312 с. http://www.twirpx.com/file/1935874/
2. Подчукаев В.А. К задаче определения области возможных состояний нестационарной линейной системы //АиТ, 1976. № 7. С. 187-189. http://www.mathnet.ru/links/b0322130560c8856fd374679a3bac2f7/at7963.pdf
3. Подчукаев В.А. Математическая модель динамического хаоса // Изв. Сарат. ун-та. Новая Серия. Сер. Математика, механика, информатика. 2012. Т. 12. Вып. 4. С. 27-31.

http://www.mathnet.ru/links/931574ba5c3b0275537ef47bcb335777/isu328.pdf

1. Подчукаев В.А. Количество вращения скалярных полей динамических систем // Известия ВУЗов. Приборостроение. 2017. Т. 60. № 12. С. 1112-1118. DOI: 10.17586/0021-3454-2017-60-12-1112-1118. http://pribor.ifmo.ru/file/article/17332.pdf
2. Брянцева О.В., Подчукаев В.А. Исследование скалярных полей динамических систем//Известия ВУЗов. Приборостроение. 2016. Т. 59, № 9. С. 723-728. DOI: 10.17586/0021-3454-2016-59-9-723-728. http://pribor.ifmo.ru/file/article/15985.pdf
3. Podchukaev V.A. Scalar and Bitorsion Biofields of String Volume Resonators Aura // 2018 14^th International Scientific-Technical Conference on Actual Problems of Electronic Instrument Engineering (APEIE) – 44894 Proceedings. APEIE — 2018. V. 1. Part 1. P. 144-146.
4. Вышнеградский И.А. Публичные популярные лекции о машинах: О теории механизмов без формул. М.: Книжный дом «ЛИБРОКОМ», 2015. 448 с.