Постановка проблемы. Задача организации высокопроизводительных вычислений является одной из определяющих для вычислительных систем. Успешное решение этой задачи позволяет получить хорошие результаты в различных отраслях науки и техники. Для создания высокопроизводительных систем необходимо решение комплекса мер с одновременным учетом ограничений по потребляемой мощности, стоимости, размеру кристалла, надежности функционирования [1]. Важной составляющей достижения эффективных вычислений являются параллельные алгоритмы [2].
Другой важной составляющей высокопроизводительных вычислений является многооперандное сложение, которое служит основой таких арифметических операций, как умножение и деление [3]. Многооперандное сложение является фундаментальной проблемой в цифровых вычислительных устройствах [4,5]. Оно широко используется криптографии — в блочном шифровании и хэш-функциях [6], а также в работе цифровых фильтров, для сжатия видео и других областях. [7]. Использование традиционных сумматоров в умножителях для суммирования промежуточных результатов ведет к превышению площади микросхем и временным задержкам [6]. Многооперандное сложение и компрессорные деревья сокращают временные задержки без сильного превышения площади [6].
Еще одной важной составляющей высокопроизводительных вычислений являются табличные методы вычислений. Они широко применяются в вычислительной технике благодаря высокому быстродействию, однако обеспечивается оно ростом оборудования для выполнения дополнительных арифметических операций. Табличные методы используются для высокоскоростной аппроксимации элементарных функций [8,9,10].
Следующей важной составляющей высокопроизводительных вычислений является применение избыточных систем счисления, которые рассматриваются как альтернатива для реализации многооперандного сложения [11], так как они обладают свойством не использовать или ограниченно использовать переносы [12, 13, 14]. Избыточное представление сокращает время сложения ограничением длины цепочек распространения переносов [7]. Поэтому для эффективной реализации многооперандного сложения широко используются избыточные сумматоры [7]. Преобразование в неизбыточное представление происходит путем сложения строки суммы и строки переносов с помощью традиционного сумматора с распространением переносов (carry propagate adder-CPA) [7].
Для дальнейшего увеличения быстродействия многооперандных сумматоров необходимо уменьшать время распространения цепочек переносов и время генерации суммы путем применения избыточных систем счисления и схемных реализаций многооперандного суммирования.
Анализ последних исследований и публикаций. Безизбыточные позиционные системы счисления не могут обеспечить полностью параллельное (а значит и наиболее быстрое) сложение [15]. Поэтому в умножителях и делителях избыточное кодирование достаточно широко используется как внутреннее, так как в нем сложение выполняется без распространения переносов за малый устойчивый промежуток времени, независимый от длин операндов [15]. Например, делитель процессора Pentium использует две различные избыточные системы счисления: итерации деления выполняются в системах счисления с сохранением переноса, а частное сначала вычисляется в системе счисления с базисом 4 с цифрами от -2 и 2 и затем конвертируется в обычную двоичную систему счисления. Итак, избыточные системы счисления уменьшают сложность арифметических алгоритмов, повышают быстродействие и надежность вычислений [15].
В работе [16, табл.1] предложены правила совмещенного во времени сложения 50-ти целых положительных чисел в линейной избыточной рекуррентной системе счисления (ЛИРССЧ) 3-го порядка, образованной на основе рекуррентного соотношения вида
![]()
с алфавитом {0, 1} и начальными значениями 1 1 1 1 2 4 8, то есть B0 = 1, B1 = 1, B2 = 1, B3 = 1, B4 = 2, B5 = 4, B6 = 8. Здесь n – номер разряда, Bn – вес разряда. Эти правила обеспечивают бесконфликтную расстановку единиц в младшие разряды сумм соответствующих старших вертикальных разрядных срезов (ВРС).
В [17] показано, что программные модели одновременного многооперандного сложения в ЛИРССЧ (1) для различного количества 16-разрядных целых положительных чисел требуют во много раз меньше разрядов для хранения промежуточных результатов вычислений и во много раз быстрее, чем соответствующие модели сложения по алгоритму Уоллеса в обычной двоичной системе счисления. Например, при сложении 10-ти 16-разрядных операндов в ЛИРССЧ (1) требуется в 1,86 раза меньше сохраняемых промежуточных значений [17], при сложении 20-ти 16-разрядных операндов – в 3,1 раза меньше сохраняемых промежуточных значений [17], а при сложении 50-ти 16-разрядных операндов – в 7,3 раза меньше сохраняемых промежуточных значений [17] по сравнению со сложением по алгоритму Уоллеса. Вследствие этого во столько же раз упростится аппаратная реализация сложения и соответственно повысится быстродействие.
Полученные результаты [17, рисунки 3 и 4] дают возможность увеличить число операндов до 1000 в совмещенном многооперандном суммировании путем соответственного увеличения числа правил рекуррентного сложения в ЛИРССЧ (1). С увеличением количества одновременно складываемых чисел до 1000 хранение в памяти этих правил становится аппаратно затратным вследствие увеличения времени доступа к каждому рекуррентному правилу.
Цель статьи. Для нахождения компромиссного решения между быстродействием многооперандного сумматора и аппаратными затратами на хранение и обработку правил сложения в линейной избыточной рекуррентной системе счисления 3-го порядка разработать алгоритм генерации каждого правила для совмещенного во времени сложения до 1000 операндов. Полагается, что до начала совмещенного во времени сложения заданного количества чисел уже известна разрядность суммы единиц каждого ВРС.
Изложение основного материала. В работе [17] приведен результат применения в программной модели правил совмещенного многооперандного сложения 20-ти целых положительных чисел в ЛИРССЧ (1) (рисунок 1).
В этой ЛИРССЧ используется диагональная запись суммы каждого ВРС, определяемая системой правил для совмещенного во времени сложения 20-ти операндов, причем каждому разряду суммы ВРС отвечает свой горизонтальный ряд начальных значений
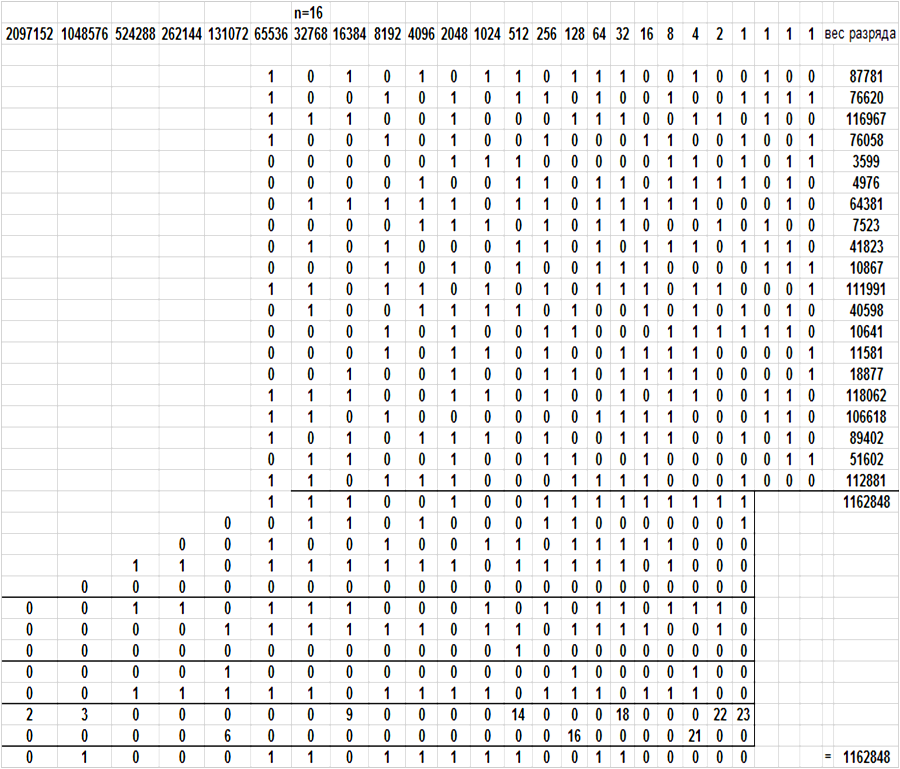
Рисунок 1. Результат применения правил совмещенного многооперандного сложения 20-ти целых положительных чисел в ЛИРССЧ (1).
Длина разрядной сетки каждой суммы ВРС зависит от числа слагаемых и определяется формулой [17]:
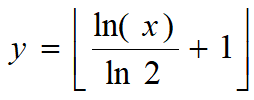
где x – количество слагаемых в десятичной системе счисления, y – разрядность числа x в двоичной системе счисления, обозначает округление с отбрасыванием дробной части числа, поскольку число разрядов является целым. Графически зависимость длины разрядной сетки каждой суммы ВРС от числа одновременно суммируемых чисел приведена на рисунке 2. Из графика видно, что существуют достаточно большие интервалы значений количества одновременно суммируемых чисел, в которых не изменяется разрядность сумм единиц в каждом ВРС, а значит и не усложняется аппаратная реализация сумматора. Из рисунка 2 также следует, что чем больше разрядность суммы каждого ВРС, тем шире интервалы одновременно суммируемых чисел. Например, для одновременного суммирования от 512 до 1000 слагаемых разрядность ВРС равна 10
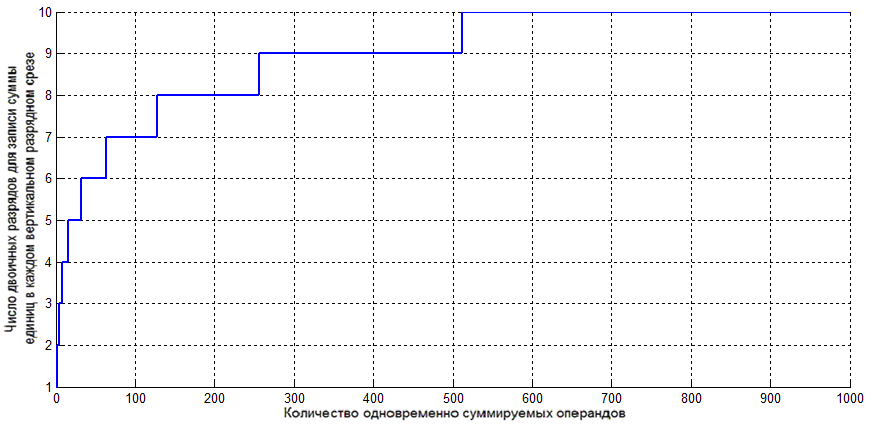
Рисунок 2. График зависимости числа разрядов для записи суммы единиц в каждом ВРС от количества одновременно суммируемых чисел.
Вследствие большого объема таблицы правил сложения (до 1000 правил) возможно применение компромиссного варианта между быстродействием и объемом памяти. С целью удешевления вычислительного устройства возможно создание схемного решения генерации любого из 1000 рекуррентного правила сложения.
Задержка генерации правила сложения должна быть меньше задержки нахождения правила в большой таблице правил сложения (до 1000 правил).
При генерации правила сложения возведение в степень основания системы счисления не используется для сокращения аппаратных и временных затрат. Память устройства генерации правила сложения до начала генерации правила содержит числа 0,![]() , При этом максимальное число складываемых чисел не должно превышать
, При этом максимальное число складываемых чисел не должно превышать ![]() .
.
Для генерации правила сложения используются только операции сравнения и вычитания. Результатом генерации правила является неубывающий набор натуральных чисел и числа 0, меньших или равных m. Числа из этого набора являются номерами i в слагаемых ![]() правила, отсчитываемыми от
правила, отсчитываемыми от ![]() для которого
для которого ![]() .
.
Далее представлен алгоритм вычисления каждого рекуррентного правила на псевдокоде:
Input: ![]() максимальное число складываемых чисел.
максимальное число складываемых чисел.
Output: ![]() — рекуррентное правило сложения
— рекуррентное правило сложения

Примеры генерации рекуррентных правил сложения в ЛИРССЧ(1) по вышеуказанному алгоритму приведены в таблице 1.
Таблица 1
| № правила | Правило |
| 1 | 0=0+0 |
| 2 | Bn=Bn+0 |
| 3 | 2Bn=Bn+1 |
| 4 | 3Bn= Bn+Bn+1 |
| … | … |
| 35 | 34Bn= Bn+1+Bn+5 |
| 36 | 35Bn= Bn+Bn+1+Bn+5 |
| 37 | 36Bn= Bn+2+Bn+5 |
| 38 | 37Bn= Bn+Bn+2+Bn+5 |
| … | … |
| 48 | 47Bn=Bn+Bn+1+Bn+2+Bn+3+ Bn+5 |
| 49 | 48Bn= Bn+4+Bn+5 |
| 50 | 49Bn= Bn+Bn+4+Bn+5 |
| 51 | 50Bn= Bn+1+Bn+4+Bn+5 |
| … | … |
| 188 | 187Bn=Bn+Bn+1+Bn+3+Bn+4+Bn+5+Bn+7 |
| … | … |
| 225 | 224Bn= Bn+5+Bn+6+ Bn+7 |
| … | … |
| 293 | 292Bn=Bn+2+Bn+5+ Bn+8 |
| … | … |
| 301 | 300Bn= Bn+2+Bn+3+ Bn+5+Bn+8 |
| … | … |
| 358 | 357Bn=Bn+Bn+2+Bn+5+Bn+6+Bn+8 |
| … | … |
| 492 | 491Bn=Bn+Bn+1+Bn+3+Bn+5+Bn+6 +Bn+7+Bn+8 |
| … | … |
| 501 | 500Bn=Bn+2+Bn+4+ Bn+5+ Bn+6 +Bn+7+Bn+8 |
| … | … |
| 898 | 897Bn=Bn+ Bn+7+Bn+8+Bn+9 |
| … | … |
| 1001 | 1000Bn=Bn+3+ Bn+5+ Bn+6 +Bn+7+Bn+8+Bn+9 |
Важной особенностью правил представленных в таблице 1 есть то, что они предотвращают неконтролируемый процесс распространения цепочек единиц переноса, так как обладают свойством бесконфликтной расстановки единиц сразу в несколько разрядов большего веса. Эти правила исключают потерю промежуточных значений при вычислении суммы, то есть обеспечивают бесконфликтное многооперандное совмещенное сложение.
Выводы. Для многооперандного сложения в пределах 1000 целых чисел компромиссным решением между быстродействием многооперандного сумматора и аппаратными затратами на хранение и обработку правил рекуррентного сложения в нем является создание устройства генерации правил рекуррентного сложения. Алгоритм генерации этих правил использует только операции сравнения и вычитания. Эти правила используются для сложения в каждом вертикальном разрядном срезе массива суммируемых чисел и не допускают неконтролируемое распространение цепочек единиц переносов благодаря свойству бесконфликтной расстановки единиц сразу в несколько разрядов большего веса.